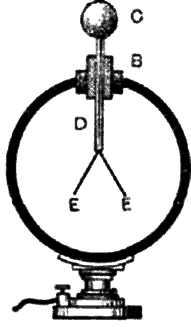
Рис. 36. Схема электроскопа: А — корпус, В — изолятор, С -шар, D — стержень, Е — лепестки.
Можно подобрать схему, отвечающую этой задаче. Для этого введём в схему многозвенника ещё электрозаряды— С и D противоположного знака по отношению к зарядам А и В. Выберем количество электрозарядов в точках А, В, С и D так, чтобы звенья нашего ромба находились в равновесии (пунктирная схема).
Теперь отнимем от молекул С и D по одному заряду, Тогда заряды D и С будут слабее отталкиваться друг от друга, и равновесие в фигуре нарушится. Для того чтобы восстановить равновесие, к точкам С и D надо приложить силу, способную поднять гирю, тогда во всех звеньях молекул вновь наступит равновесие.
Согласно закону сохранения энергии, работа, затраченная на подъем груза на высоту, будет равна энергии двух отнятых электрозарядов у С и D.
Такую схему можно рассчитать. Она полностью удовлетворяет требованию пункта 1 технического задания.
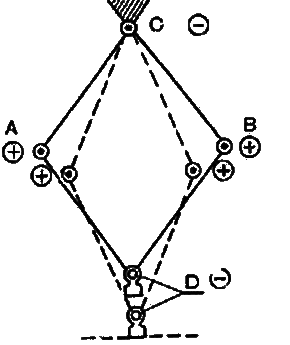
Рис. 37. Схема ромбоидального силового многозвенника: А и В — положительные заряды, С и D — отрицательные заряды.
Любопытно, что сжать в поперечном направлении этот силовой ромб мешают силы взаимоотталкивания зарядов А и В. Но как только мы перестанем сжимать ромб, силы противодействия нашим пальцам исчезают, так как все силы в ромбе уравновешены. Это свойство схемы отвечает требованию пункта 2.
Итак, предлагаемую ионную силовую электромолекулярную схему примем в качестве одного из рабочих вариантов для решения нашей задачи в целом.
Теперь перейдём к рассмотрению проектируемого нами предварительного механизма мышечного сокращения.
На рис. 38 изображена мышца (бицепс) руки человека. Для упрощения задачи первоначально заменим её схемой в виде геометрической фигуры шарнирного многозвенника удлинённого ромба. На углах по горизонтали сосредоточим скопление положительных ионов, по вертикали — отрицательных. Одноимённые заряды отталкиваются, а разноимённые притягиваются. Заряды 1 — 1 и 7-7 на углах ромба подобраны так, что все равнодействующие силы Кулона в многозвеннике уравновешиваются. По расчёту это наступает при условии, если положительные заряды содержат по одному заряду, а отрицательные по 7 зарядов и угол в вершине ромба равен 30° (отношение числа зарядов 1:7).
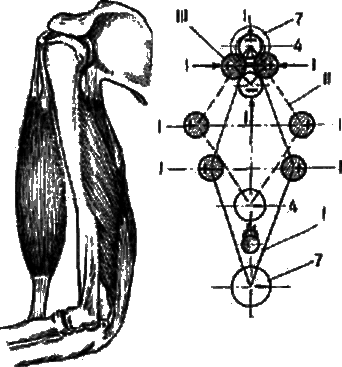
Рис. 38. Условная замена силовым ионным ромбоидальным многозвенникои мышцы руки человека.
Для того чтобы поднять гирю, надо согласно диаграмме (см. рис. 12) убавить число свободных отрицательных зарядов, то есть убавить определённое число электронов, например, с 7-7 до 4-4. Тогда уменьшенные отрицательные заряды 4-4 будут отталкиваться слабее. Следовательно, для нового равновесия сил в многозвеннике необходимо добавить вес гири, которая слегка поднимается над столом. Для того чтобы поднять её ещё выше, необходимо ещё больше сократить число отрицательных зарядов и т.д.
Аналогичное постепенное разряжение мышцы мы наблюдаем на диаграмме (см. рис. 12. участок Б-В) при постепенном подъёме гири рукой. Следовательно, для удержания одного и того же груза при разной степени сокращения мышцы требуется различное число зарядов в мышце. Изменение углов в многозвеннике это подтверждает. Таким образом, пункт первый нашего технического задания схема удовлетворяет.
Согласно закону сохранения энергии работа подъёма гири на данную высоту должна быть равна энергии отнятых из многозвенника электронов за вычетом потерь. Пункт 2 удовлетворён.
Чем больше отнимается отрицательных зарядов, тем больше многозвенник приближается к квадрату (см. рис. 38, III). Когда число отрицательных и положительных зарядов уравняется, то есть во всех углах останется по одному заряду, многозвенник превратится в квадрат и равнодействующие всех электрических сил (расчёт подтверждает это) заставят ионы, расположенные на углах квадрата, притянуться друг к другу до соприкосновения молекул с такой силой, что мышца превратится в твёрдое тело, Мы наблюдаем это явление при контрактуре, когда кровообращение прекращается, окислительные реакции в мышцах нарушаются, все свободные отрицательные заряды нейтрализуются и остаётся только нейтральная ионизированная среда, в которой число положительных и отрицательных ионов равно (ионная симметрия).
Пункт 8 удовлетворяется.
Для того чтобы судить об огромной величине сил Кулона — взаимопритяжения электрозарядов, достаточно сказать, что два разноимённых заряда с количеством электричества по одному кулону, удалённые друг от друга на расстояние в один километр, притягиваются с силой в 0,9 тонны.
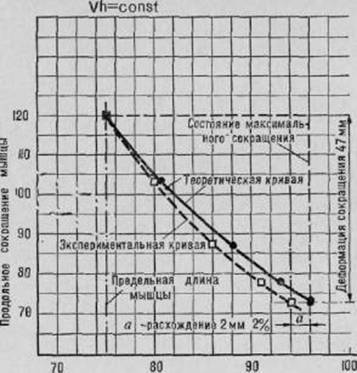
Рис. 39. Диаграмма сравнения теоретической кривой соотношения длины и ширины мышцы с кривой, полученной при эксперименте.
Теперь надо подумать, куда из мышцы после смерти человека направляются отнятые свободные заряды и где они нейтрализуются.
В пункте 10 сказано, что после перерезки нервов контрактура не наступает. Следовательно, свободные заряды из мышц при контрактуре могут направиться по электропроводным нервам в содержащее положительные заряды мозговое вещество. Если нерв перерезан, заряды не уйдут и контрактура не наступит. После нейтрализации всех зарядов и окончания трупного окоченения мышцы снова расслабляются осмотическими силами.
При сокращении длины мышцы мы наблюдаем увеличение её поперечного размера по экспериментальной кривой, изображённой на диаграмме (рис. 39).
Здесь же нанесена закономерная теоретическая кривая изменения поперечного размера х нашего ромба-многозвенника при сокращении его длины по уравнению х? у=УК=const. Разница кривых не превышает 2%. Это говорит в пользу гипотезы многозвенника. Пункт 5 удовлетворён.
В поперечном сечении напряжённую мышцу трудно сжать. Пальцы встречают сильное противодействие Откуда возникают такие удивительные силы в мышце? Схема многозвенника это объясняет. Чтобы сжать в поперечном сечении мышцу, надо сблизить уравновешенные положительно заряженные ионы 1-1 многозвенника (см. рис. 38). Но это сделать очень трудно, так как силы Кулона — взаимоотталкивания этих одноимённых зарядов — препятствуют их сближению. Пункт 6 удовлетворяется.
Следовательно, силовой ромб (в первом приближении) правдоподобен. Предложенная схема показывает, что так мог бы выглядеть элементарный мышечный электродвигатель на молекулярном уровне.
Но дело усложняется тем, что ромб — это фигура плоскостная, а тонкая протофибрилла в мышце — объёмная трубочка (оболочка), заполненная плазмой и молекулами. Для того чтобы силовой ромб стал объёмной фигурой, ему надо придать вращение вокруг вертикальной оси. Тогда он превратится в два конуса с общим основанием, где расположатся положительные заряды, а в вершинах окажутся отрицательные, по-прежнему в отношении 1:7. Цепочка таких конусов (рис 40 I) и будет представлять силовой каркас объёмных тонких протофибрилл. Но они содержат в семь раз больше отрицательных зарядов, чем положительных, а это привело бы к появлению в мышце огромного свободного электрозаряда. Этого в мышцах не наблюдается значит, где-то рядом с отрицательными зарядами должно располагаться равное количество положительных зарядов, и действительно, с помощью электронного микроскопа можно увидеть, что в центре расположения шести тонких протофибрилл помещается толстая протофибрилла, отделённая от них оболочкой. Для того чтобы в мышце все свободные отрицательные заряды тонких протофибрилл были компенсированы, необходимо, чтобы в толстых протофибриллах цепочки конусных многозвенников имели зеркальное расположение зарядов, то есть в вершинах конусов — положительные заряды, а в основаниях — отрицательные (рис. 40, II). На рис. 40, IV показаны фотография Т. Хайаши, снятая электронным микроскопом с увеличением в 250 000 раз (видны толстые (тёмные) и тонкие (светлые) протофибриллы), и рядом схема автора (рис. 40, III). Для сокращения мышцы надо убавить число зарядов в вершинах конусов. Этого можно достигнуть, удалив часть отрицательных зарядов из тонких протофибрилл и нейтрализовав ими часть положительных зарядов в толстых протофибриллах. Но между толстыми и тонкими протофибриллами находятся оболочки. Как же они устроены, если эта нейтрализация происходит только тогда, когда я «хочу» сократить мышцу?