— Эх вы, теоретики! — поддразнила Таня. — Лучше подсчитайте, что должен был заплатить Магистр за своего верблюда и что Единичка — за своего.
— Это мы могим! — весело согласился президент и принялся писать веточкой на снегу. — Сперва сделаем все возможные перестановки цифр в числе 165. Вот они. 165, 156, 561, 516, 651 и 615. Теперь сложим эти числа. Получим. Не мешайте, а то я собьюсь получим 2664. Проверим.
— И проверять нечего, всё верно, — торопила Таня.
— Теперь подсчитаем, что должна была Заплатить Единичка, — сказал Сева. — Вот перестановки цифр числа 732: 732, 723, 273, 237, 327 и 372. Сложим их и получим что такое! Тоже 2664
— В чём же дело? — недоумевал президент. — Выходит, в этом случае любое трёхзначное число даст один и тот же результат? Или, может быть, 165 и 723 — числа специально подобранные?
— Уж конечно, специально, — сказала Таня
— Вот это да! Значит, проезд на любом верблюде стоил одинаково. Но как же удалось подобрать такие числа?
— А ты посмотри на них внимательней, — посоветовала Таня — Не найдётся ли у них какого-нибудь общего признака?
— Найдётся! — отвечал президент весьма язвительно. — Все цифры у них разные.
— Цифры действительно разные, — подтвердила Таня, — зато сумма этих цифр одна и та же. 12.
— Верно! — обрадовался Нулик. — 1 + 6 + 5 = 12. И 7 + 3 + 2 тоже равно двенадцати. Может быть, то же свойство было и у всех других чисел на верблюжьих табличках?
— Очень возможно. Недаром Единичка сказала, что погонщики в Террапантере — народ справедливый.
— И всё-таки. — Нулик сделал непреклонное лицо, — всё-таки я требую доказательства.
— Сей момент, ваше президентство! — насмешливо поклонилась Таня. — Будет сделано. Запишем любое трёхзначное число в общем виде. Это 100a + 10b + c. Понятно?
— Что за вопрос? Конечно! Здесь а — число сотен, b — число десятков, с — число единиц.
— Гениально! Теперь сделаем в этом числе все возможные перестановки цифр Напишем их сразу столбиком, а потом сложим.
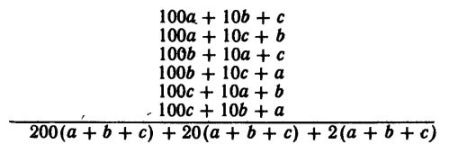
— Не желаете ли, ваше президентство, преобразовать эту сумму? — спросила Таня.
— Желаю, — отвечал его президентство без особого энтузиазма. — Я бы я бы вынес 2(а + в + с) за скобки.
— Совершенно с вами согласна. Получится при этом:
2 (а + b + c) (100 + 10 + 1)
— А это всё равно что 222 (а + b + с), — подсчитал Нулик. — Но что из этого следует?
— Только то, что сумма перестановок зависит не от самого числа, а от суммы его цифр. И значит, все трёхзначные числа с одинаковой суммой цифр в этом случае всегда будут давать одно и то же число.
— Ха-ха! — выдохнул президент, несколько подавленный роскошным Таниным доказательством. — Выходит, для всех трёхзначных чисел с суммой цифр, равной двенадцати, ответ будет всегда 222X12, то есть 2664. Теперь хорошо бы ещё узнать, что получится, если взять четырёх-, пяти- или двенадцатизначные числа.
— Да то же самое, — сказала Таня, — только численный результат будет другой.
— Обязательно займусь этим на досуге! Жаль, досуга у меня маловато, — проворчал Нулик, постукивая ногой об ногу и выразительно поглядывая на уютные окна кафе, мимо которого мы как раз проходили.
Это было понятно, как безмолвный сигнал к атаке, и через мгновение мы уже находились внутри, за стеклянной дверью.
В кафе было тепло и, к счастью, безлюдно. Я говорю — к счастью, потому что Нулик, предвкушая лакомое угощение, взыграл и принялся носиться между столиками, описывая вокруг них замысловатые фигуры.
— Это я плутаю по лабиринту, — объяснил он, — скоро доберусь до мини-Тавра. Только вот где найти цепочку Афродиты?
Олег комически схватился за голову
— Опять этот младенец повторяет ошибки Магистра!
— Ничуть не бывало! — выкрутился президент. — Просто я вас подначиваю. Из педагогических соображений.
Олег понимающе кивнул.
— Из педагогических, говоришь? Ну, тогда тебе, стало быть, известно, что произносить надо Минотавр. И это тебе не мини, а совсем даже наоборот огромное чудище. Получеловек, полубык.
— А разве такие бывают? — наивно спросил Нулик, сразу позабыв о педагогических соображениях.

— Если верить древнегреческому мифу, один, во всяком случае, имелся. В давние времена, на острове Крит, у царя Миноса. Этот самый Минос построил на Крите такой лабиринт, что выбраться оттуда не было никакой возможности. Здесь и поселил царь своего прожорливого и свирепого человеко-быка, а в пищу ему отправлял провинившихся и обречённых в жертву богам людей. Плутая по запутанным коридорам, те в конце концов неминуемо попадали в пасть к Минотавру.
— Безобразие! — возмутился Нулик. — Неужели никто с этим чудищем не справился?
— Представь себе, такой человек нашёлся. Звали его, Тезей.
— Тезей, — повторил Нулик, хихикнув. — Тезей-ротозей
— То-то и оно, что не ротозей. Тезей сумел-таки разделаться с Минотавром и выбрался из лабиринта.
— С помощью цепочки Афродиты?
— Да нет, греческая богиня Афродита тут ни при чём. Помогла Тезею дочь Миноса — Ариадна. Она дала ему клубок ниток. Тезей, как вошёл в лабиринт, так сразу стал разматывать этот клубок. А когда победил Минотавра, пошел обратно вслед за нитью, сматывая её по пути. Так нить вывела его на свободу. Отсюда и пошло выражение «нить Ариадны» — нить, которая помогает выбраться из запутанных, затруднительных обстоятельств.
Президент озабоченно поджал губы.
— Теперь без катушки ниток в кармане шагу не сделаю! Мало ли что.
Опасения его были прерваны официанткой, которая спросила, что нам принести. Я заказал кофе, слоёных пирожков и трубочек с кремом.
Нулик опасливо зыркнул глазом.
— Боюсь, у меня на такой пир пресмыкающихся не хватит.
— Чего чего? — недоуменно переспросил Сева.
— Ну, скарабеев, — объяснил президент и очень обиделся, когда все дружно захохотали.
— Нет, он меня уморит! — сказал Сева, утирая глаза. — Какие же скарабеи — пресмыкающиеся? Они же вовсе насекомые. Попросту навозные жуки. А их, между прочим, в Древнем Египте считали священными и потому изображали на кольцах, печатях, всяких амулетах. Считалось, что скарабей приносит счастье.
— Да ну?! — Президент даже подпрыгнул. — Хочу скарабея, хочу скарабея! — затараторил он, как Буратино.

Пришлось мне призвать его к порядку.
— Ты где находишься?
— В кафе.
— Так и веди себя соответственно. А хочешь говорить, так говори что-нибудь дельное. Вот хоть разберись в задаче со скарабеями.
Но охота говорить у президента почему-то разом прошла, и за дело взялся Сева. Выступление его было кратким — оно и понятно, он решал задачу алгебраическим способом.
— Число скарабеев, принесенных Чёрным Львом, обозначим буквой а. Тогда число скарабеев, добытых Мистером-Твистером, равно 2а — ведь у него их было вдвое больше! Число скарабеев, которых отнял у Чёрного Льва Джерамини, обозначим через икс. Выходит, что у этого Льва осталось
— …(а — х) скарабеев, — подсказала Таня.
— Верно. А так как у Мистера-Твистера Джерамини отнял в три раза больше скарабеев, чем у Чёрного Льва, число это равно Зх. И значит, осталось у него (2а — Зх). скарабеев. Известно, что после этого грабежа у обоих полицейских денег оказалось поровну. Поэтому мы можем смело приравнять (а — х) и (2а — 3х). Вот вам и уравнение (а — х) = (2а — 3х). Ну, президент, включайся, решай!
Нулик надулся.
— Да, оставили мне самое неинтересное.
Но всё-таки обиженно засопел над блокнотом.
— Переносим неизвестные в одну часть равенства, а известные — в другую. Тогда 2х = а. Отсюда х = 1/2а. Что из этого вытекает? — Глаза президента вдруг оживились, голос окреп. — Из этого вытекает, что Джерамини заграбастал половину львиного богатства.