Пространство де Ситтера обладает горизонтом событий, так же как и черная дыра. Если вы приблизитесь к черной дыре и перейдете роковую черту, она втянет вас внутрь, и вы уже не вернетесь домой к ужину. То же верно и в отношении света, который не сможет покинуть дыру. Это также верно и в случае горизонта де Ситтера. Если зайти слишком далеко в пространство, которое расширяется с ускорением, то вы никогда не сможете вернуться в точку, откуда стартовали. Свет, как и в случае черной дыры, тоже не сможет вернуться назад.

Когда космологическая постоянная мала, а ускоренное расширение происходит относительно медленно, что имеет место в современном мире, горизонт находится очень далеко. Вот почему объем этого пространства такой большой. И наоборот, если космологическая постоянная велика, а Вселенная расширяется с огромной скоростью, то горизонт (или критическая точка) может находиться очень близко — чуть ли не под рукой (в буквальном смысле), и объем соответственно будет мал. «Если вы засунете вашу руку слишком далеко в такое пространство, — объясняет Линде, — то быстрое расширение может оторвать вам ее».[217]

Хотя энтропия пространства де Ситтера коррелирует с объемом, правильнее будет сказать, что она коррелирует с площадью поверхности горизонта событий, которая определяется расстоянием (точнее, квадратом расстояния) до горизонта. Фактически, можно использовать то же обоснование и формулу Бекенштайна-Хокинга, что мы применяли к черным дырам в восьмой главе, то есть энтропия де Ситтера пропорциональна площади горизонта, деленной на четыре ньютоновские гравитационные постоянные G. Расстояние до горизонта, или, формально, — квадрат расстояния, в свою очередь зависит от космологической постоянной: чем больше значение космологической постоянной, тем меньше расстояние. Поскольку энтропия соизмерима с квадратом расстояния, а квадрат расстояния обратно пропорционален космологической постоянной, то энтропия также будет обратно пропорциональна космологической постоянной. По Хокингу, верхний предел для космологической постоянной в нашей Вселенной составляет 10^-120 в «безразмерных единицах», которые используют физики.[218] Число 10^-120 является грубым приближением, его не следует воспринимать как точную цифру. Энтропия, будучи обратно пропорциональной космологической постоянной, получается чрезвычайно большой — примерно 10¹²⁰, как упоминалось выше. Энтропия по определению равна не числу состояний, а натуральному логарифму числа состояний. Поэтому количество состояний фактически равно e^{энтропия}. Вернемся к графику на рис. 11.1, где число возможных состояний в нашей Вселенной с небольшой космологической постоянной, которая (Вселенная) представлена локальным минимумом на кривой, составляет e^(10???).

Предположим, что поверхность горной вершины, с которой объект скатывается вниз к измерениям бесконечного радиуса, является таким исключительным местом, где существует только одно состояние, которое доставит вас точно на вершину. Поэтому вероятность посадки в этом конкретном месте среди всех других вероятностей исчезающе мала — порядка 1/e^(10???). Вот почему время туннелирования через барьер является настолько большим, что мы даже не можем назвать его астрономическим.

Еще одно замечание: на рис. 11.2 мы представили сценарий декомпактификации, при котором наша Вселенная туннелирует до состояния с более низким значением энергии вакуума (или меньшей космологической постоянной), делая промежуточную остановку на ландшафте во время своего путешествия к конечной перестройке — бесконечным радиусам измерений. Но можем ли мы, туннелируя, отправиться обратно, к месту с более высокой энергией вакуума? Безусловно, катиться под гору намного проще. Можно показать это следующим рассуждением. Предположим, что имеется потенциальный минимум в точке A и отдельный минимум в точке В, причем точка А расположена выше, чем В, а следовательно, имеет большую энергию вакуума. Поскольку в точке А более высокая энергия, то сильнее и гравитация, и пространство в ней будет иметь более высокую кривизну. А если мы будем рассматривать это пространство как сферу, ее радиус будет меньше, поскольку сферы меньших размеров имеют большую кривизну, чем сферы больших размеров. Поскольку в точке В более низкая энергия, то гравитация будет слабее. Следовательно, пространство вокруг нее будет иметь меньшую кривизну. А если мы будем рассматривать это пространство как сферу, ее радиус будет больше, и поэтому она будет обладать меньшей кривизной. Мы проиллюстрировали некоторые аспекты этой идеи на рис. 11.3 (используя для А и В ящики, а не сферы), чтобы показать, что объект, вероятнее всего, путешествует вниз к ландшафту с более низкой энергий — от А к В, чем вверх. Для большей наглядности можно соединить два ящика тонкой трубкой. Эти два ящика со временем придут в равновесие и будут иметь одинаковую концентрацию, или плотность, газов, а количество молекул, переходящих из А в В, будет равно количеству молекул, переходящих из В в А.

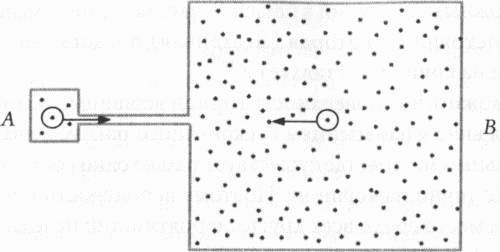
Рис. 11.3. На этом рисунке сделана попытка показать, почему легче «туннелировать вниз» от А к В (см. рис. 11.2), а не «туннелировать вверх» от В к А. Аналогия, представленная здесь, показывает, что обнаружить молекулу в В более вероятно, чем в А, просто потому, что количество молекул в В гораздо больше, чем в А

Однако поскольку В намного больше, чем А, в нем намного больше молекул. Поэтому вероятность перехода любой отдельной молекулы из А в В намного больше, чем вероятность перехода отдельной молекулы из В в А. Аналогично, вероятность появления пузыря, который перенесет вас в место с низкой энергией на ландшафте, существенно выше, чем вероятность возникновения пузыря, который перенесет вас в обратном направлении (в гору), как и любая молекула с большей вероятностью совершит переход из ящика А в В.

В 1890 году Анри Пуанкаре опубликовал свою так называемую теорему о возвращении, которая утверждает, что любая система с фиксированным объемом и энергией, которую можно описать с помощью статистической механики, обладает характеристическим временем возвращения в исходное состояние, равным e^{энтропия системы}. Идея состоит в том, что такая система обладает конечным числом состояний — конечным количеством положений частиц и скоростей. Если вы будете стартовать с определенного состояния и ждать достаточно долго, то, в конце концов, достигнете всех состояний, подобно тому как частица или молекула в нашем ящике будет «брести, не разбирая дороги», отскакивая от стенок и двигаясь хаотически, со временем побывает в каждом из всех возможных мест ящика. Выражаясь научным языком, мы будем говорить не о возможных местах ящика, а о возможных состояниях в «фазовом пространстве». Тогда время, необходимое пространству-времени для декомпактификации, равно времени возвращения Пуанкаре — то есть e^{энтропия}, или e^(10???) лет. Но, по мнению Клебана, в этом доказательстве существует одно слабое звено. «Мы еще не имеем статистическо-механического описания пространства де Ситтера». При этом мы априори предполагаем (что может оказаться правдой, а может, и нет), что такое описание возможно.[219]

В настоящее время нам нечего добавить по этому вопросу, да и немногое сделано в этом направлении, за исключением, возможно, уточнения вычислений, оценок и повторной проверки нашей логики. Неудивительно, что немногие исследователи склонны работать в этом направлении и дальше, поскольку мы говорим о чрезвычайно теоретических событиях в сценариях, зависящих от модели, которые еще нельзя проверить, и сама возможность проверки появится не скоро. Работа в этом направлении вряд ли гарантирует предоставление грантов или получение молодыми исследователями признания у своих старших коллег и, что важнее, не гарантирует карьерного роста.