Естественно рождается мысль, что, углубляясь с гирей в недра Земли, т. е. приближая тело к центру нашей планеты, мы должны наблюдать усиление притяжения: гиря в глубине Земли должна весить больше. Эта догадка неверна: с углублением в Землю тела не увеличиваются в весе, а, напротив, уменьшаются.
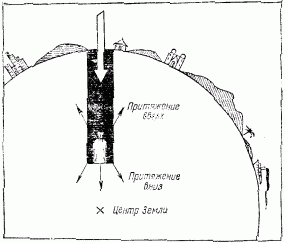
Рис. 23. Почему с углублением в Землю сила тяжести ослабевает.
Объясняется это тем, что в таком случае притягивающие частицы Земли расположены уже не по одну сторону тела, а по разные его стороны. Взгляните на рис. 23. Вы видите, что гиря, помещенная в глубине Земли, притягивается вниз частицами, расположенными ниже гири, но в то же время притягивается вверх теми частицами, которые лежат выше нее. Можно доказать, что в конечном итоге имеет значение притягивающее действие только шара, радиус которого равен расстоянию от центра Земли до местонахождения тела. поэтому вес тела по мере углубления в Землю должен быстро уменьшаться. Достигнув центра Земли, тело совсем утратит вес, сделается невесомым, так как окружающие частицы влекут его там во все стороны с одинаковой силой.
Итак, всего больше тело весит на самой поверхности Земли; с удалением от нее ввысь или вглубь вес его уменьшается [Так происходило бы, если бы земной шар был вполне однороден по плотности: в действительности плотность Земли возрастает с приближением к центру; поэтому сила тяжести при углублении в Землю сначала, на некотором расстоянии, растет и лишь затем начинает ослабевать.].
Заметили ли вы, какое странное ощущение испытываете вы в тот момент, когда начинаете спускаться на лифте? Ненормальная легкость, вроде той, какую испытывает человек, летящий в пропасть… Это — не что иное, как ощущение невесомости: в первый момент движения, когда пол под вашими ногами уже опускается, а вы сами не успели еще приобрести той же скорости, тело ваше почти не давит на пол и, следовательно, весьма мало весит. Проходит мгновение, и странное ощущение прекращается; ваше тело, стремясь падать быстрее, чем равномерно движущийся лифт, давит на его пол и, значит, снова приобретает свой полный вес.
Привесьте гирю к крючку пружинных весов и следите, куда двинется указатель, если весы с гирей быстро опустить вниз (для удобства поместите кусочек пробки в прорезь весов и заметьте изменение его положения). Вы убедитесь, что во время падения указатель показывает не полный вес гири, а гораздо меньше! Если бы весы падали свободно и вы имели возможность во время падения следить за их указателем, вы заметили бы, что гиря при падении вовсе ничего не весит: указатель находится у нуля.
Самое тяжелое тело становится совершенно невесомым в течение всего того времени, пока оно падает, Легко понять, почему это так. “Весом” тела мы называем силу, с которой тело тянет точку подвеса или давит на свою опору. Но падающее тело не производит никакого натяжения пружины весов, так как пружина опускается вместе с ним. Пока тело падает, оно ничего не натягивает и ни на что не напирает. Следовательно, спрашивать о том, сколько весит тело, когда оно падает, все равно, что спрашивать: сколько тело весит, когда оно не весит?
Еще основатель механики, Галилей, в XVII веке писал [В “Математических доказательствах, касающихся двух отраслей новой науки”. В 1934 г. вышел полный русский перевод этого замечательного сочинения.]: “Мы ощущаем груз на наших плечах, когда стараемся мешать его падению. Но если станем двигаться вниз с такой же скоростью, как и груз, лежащей на нашей спине, то как же может он давить и обременять нас? Это подобно тому, как если бы мы захотели поразить копьем [Не выпуская его из рук.Я.П.] кого-либо, кто бежит впереди нас с такой же скоростью, с какой движемся и мы”.

Рис. 24. Опыт, иллюстрирующий невесомость падающего тела.
Следующий легко исполнимый опыт наглядно подтверждает правильность этих рассуждений.
На одну чашку торговых весов положите щипцы для раскалывания орехов так, чтобы одно колено их покоилось на чашке, другое же привяжите за конец ниткой к крючку коромысла (рис. 24). На другую чашку поместите столько груза, чтобы весы были в равновесии. Поднесите к нитке зажженную спичку; нитка перегорит и верхнее колено щипцов упадет на чашку.
Что же произойдет в этот момент с весами? Опустится ли чашка с щипцами в то время, пока колено еще падает, поднимется она или останется в равновесии?
Теперь, когда вы знаете уже, что падающее тело не имеет веса, вы можете заранее дать правильный ответ на этот вопрос: чашка должна подняться на мгновение вверх.
В самом деле: верхнее колено щипцов, падая, хотя и остается в соединении с нижним, все же давит на него меньше, чем в неподвижном состоянии. Вес щипцов на мгновение уменьшается, и чашка, естественно, поднимается вверх.
В 1865 — 1870 гг. появился во Франции фантастический роман Жюля Верна “Из пушки на Луну”, в котором высказана необычайная мысль: послать на Луну исполинский пушечный снаряд-вагон с живыми людьми! Жюль Берн представил свой проект в столь правдоподобном виде, что у большинства читателей, наверное, возникал вопрос: нельзя ли в самом деле осуществить эту мысль? Об этом интересно побеседовать [Теперь, после запуска искусственных спутников Земли и космических ракет, мы можем сказать, что для космических путешествий будут использоваться ракеты, а не снаряды. Однако движение ракеты, после того как сработала ее последняя ступень, подчиняется тем же законам, что и движение артиллерийского снаряда. Поэтому текст автора не устарел. (Прим. ред.)].
Сначала рассмотрим, можно ли — хотя бы теоретически — выстрелить из пушки так, чтобы снаряд никогда не упал назад, на Землю. Теория допускает такую возможность. В самом деле, почему снаряд, горизонтально выброшенный пушкой, в конце концов падает на Землю? Потому что Земля, притягивая снаряд, искривляет его путь: он летит не по прямой линии, а по кривой, направленной к Земле, и поэтому рано или поздно встречается с почвой. Земная поверхность, правда, тоже искривлена, но путь снаряда изгибается гораздо круче. Если же кривизну пути снаряда ослабить и сделать ее одинаковой с искривлением поверхности земного шара, то такой снаряд никогда не сможет упасть на Землю! Он будет двигаться по кривой, концентрической с окружностью земного шара; другими словами, сделается его спутником, как бы второй Луной.
Но как добиться, чтобы снаряд, выброшенный пушкой, шел по пути, менее искривленному, чем земная поверхность? Для этого необходимо только сообщить ему достаточную скорость. Обратите внимание на рис. 25, изображающий разрез части земного шара.
На горе, высотой которой будем пренебрегать, в точке A стоит пушка. Снаряд, горизонтально выброшенный ею, был бы через секунду в точке B, если бы не существовало притяжения Земли. Но притяжение меняет дело, и под действием этой силы снаряд через секунду скажется не в точке B, а на 5 м ниже, в точке C. Пять метров — это путь, проходимый (в пустоте) каждым свободно падающим телом в первую секунду под действием силы тяжести близ поверхности Земли. Если, опустившись на эти 5 м, снаряд наш окажется над уровнем Земли ровно настолько же, насколько был он в точке A, то, значит, он движется по кривой, концентрической с окружностью земного шара.
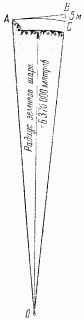
Рис. 25. Вычисление скорости снаряда, который должен навсегда покинуть Землю.
Остается вычислить отрезок АВ (рис. 25), т. е. тот путь, который проходит снаряд в секунду по горизонтальному направлению; мы узнаем тогда, с какой секундной скоростью нужно для нашей цели выбросить снаряд из жерла пушки. Вычислить это, нетрудно из треугольника АОВ, в котором ОА — радиус земного шара (около 6 370 000 м); ОС = ОА, ВС = 5 м; следовательно, 0В = 6 370 005 м. Отсюда по теореме Пифагора имеем: (AB)2 = (6 370 005)2 — (6 370 000)2.