Как уже отмечалось, для оптимизации процедур трехмерного моделирования следует:

□ рационально располагать модель относительно начала координат;

□ обоснованно выбирать плоскость проекций для создания эскиза основания модели;

□ предварительно планировать формы эскизов с целью минимизации количества формообразующих операций, необходимых для создания модели.

В табл. 10.1 представлен один из вариантов карты тестирования по теме «Построение трехмерных моделей деталей».

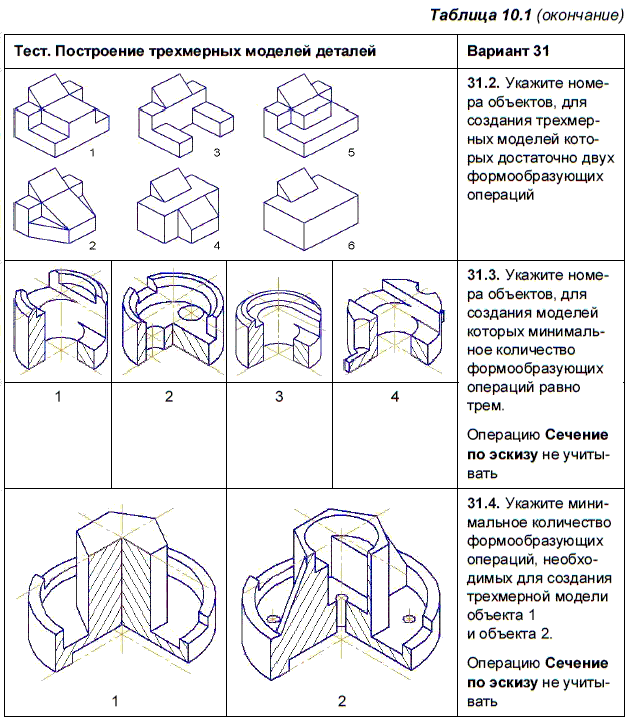
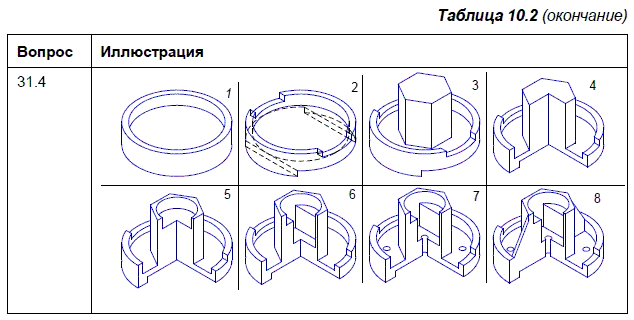
Таблица 10.2 наглядно иллюстрирует этапы построения моделей по 4 вопросам теста.

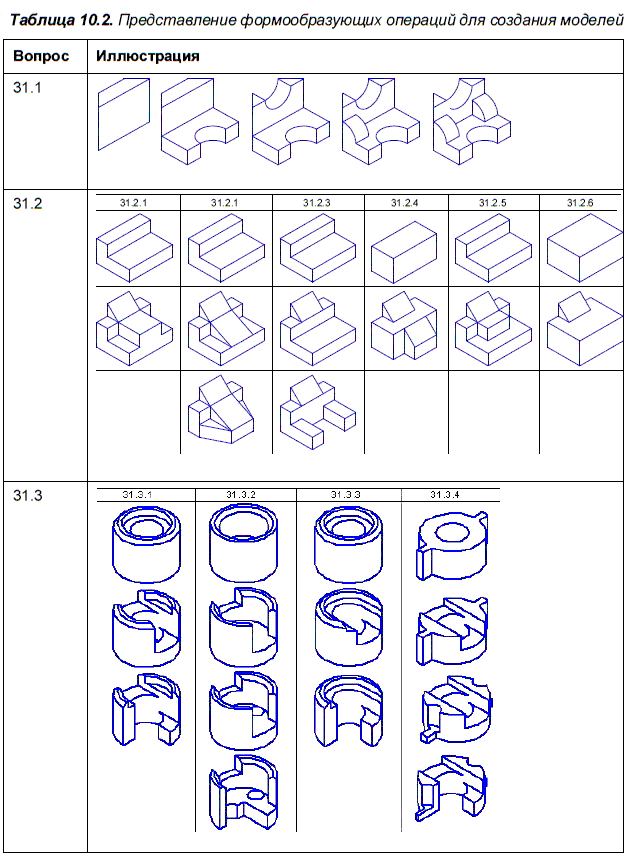
По вопросу 31.1 требуется указать минимальное количество формообразующих операций, необходимых для создания показанной детали. В разработанных вариантах теста, для создания модели достаточно от 4 до 6 формообразующих операций.

Вопросы 31.2 и 31.3 теста требуют анализа формы простых моделей, для создания которых достаточно, как правило, не более трех-четырех формообразующих операций.

Вопрос 31.4 иллюстрируются изображениями более сложных объектов. Для правильных ответов на поставленные вопросы требуется целесообразно представить дерево модели каждого объекта.

Известны успешные попытки использования, при изучении в школе геометрии, специализированных графических сред, например Windows-приложения Geometer’s Sketchpad. Альтернативы такому подходу не было, т. к. среды конечных пользователей, являвшиеся инструментами профессионалов, из-за высокой стоимости легально не применялись в образовательных учреждениях. Некоммерческое распространение учебных версий, в том числе графических пакетов, поставило вопрос о разумном выборе базового программного обеспечения, с помощью которого в общеобразовательных учреждениях решаются задачи геометрического моделирования в курсах информатики, черчения, геометрии.

Рассмотрим примеры решения школьных геометрических задач с помощью двумерного редактора КОМПАС-3В LT.

Условие. Построить квадрат по точкам А и В на серединах смежных сторон.

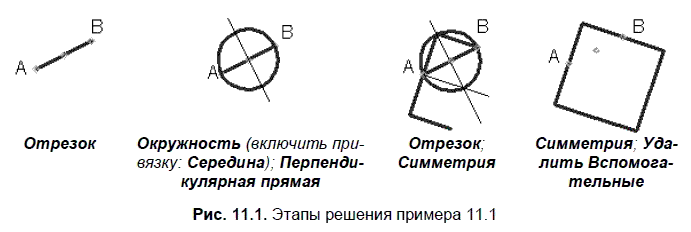
Решение. На рис. 11.1 показаны этапы построения квадрата с указанием необходимых для решения команд.

Условие. Построить квадрат по центру С и точкам А и В на одной из сторон.

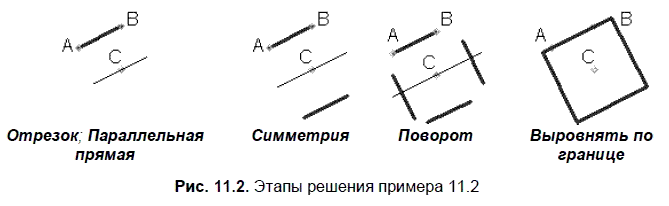
Решение. На рис. 11.2 показаны этапы построения квадрата с указанием необходимых для решения команд.

Условие. Построить квадрат AEFG, площадь которого вдвое меньше площади квадрата ABCD, а вершина F принадлежит диагонали АС.

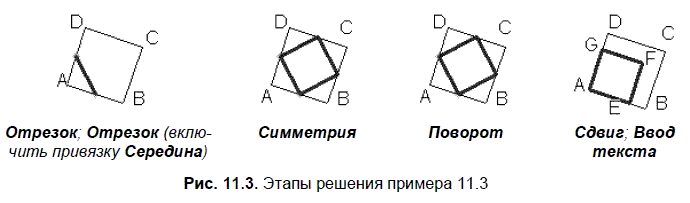
Решение. На рис. 11.3 показаны этапы построения квадрата с указанием необходимых для решения команд.

Условие. Построить параллелограмм по серединам трех сторон — точкам А, В, С.

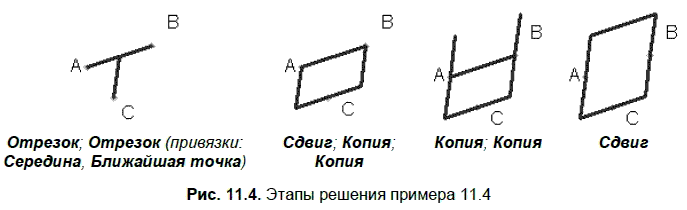
Решение. На рис. 11.4 показаны этапы построения квадрата с указанием необходимых для решения команд.

Условие. Из точки А провести к окружности диаметром D = 20 мм с центром О две касательные АВ и АС, где В и С — точки касания. /_ ВАС = φ. Определить:

□ длину отрезка О А и угол φ, если ВС = 16 мм;

□ длину отрезка ВС и угол φ, если АО = 25 мм;

□ длину отрезков ВС и АО, если φ = 80°.

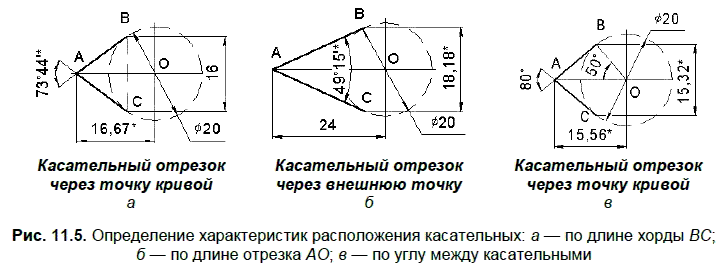
Решение. На рис. 11.5 указаны команды проведения касательных для определения искомых величин. Знаком «*» отмечены искомые величины, полученные в результате нанесения соответствующих размеров.

Условие. Стороны АВ и АС треугольника ABC являются касательными окружности радиуса R с центром О. /_ ВАС = φ. Определить:

□ радиус R и длину отрезка ОА, если ВС = 16 мм, φ = 50°;

□ радиус R и длину отрезка ВС, если АО = 20 мм,φ = 50°;

□ радиус R и угол ср, если АО = 30 мм, ВС =18 мм.

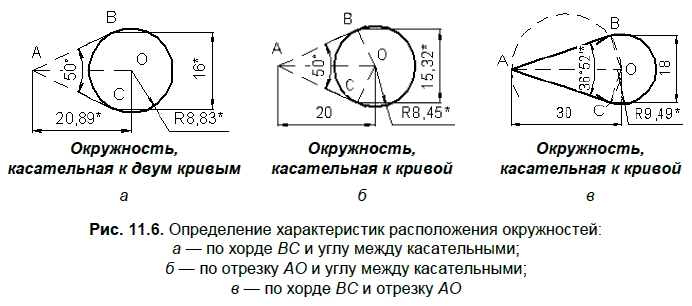
Решение. На рис. 11.6 указаны команды проведения окружностей для определения искомых величин. Знаком «*» отмечены искомые величины, полученные в результате нанесения соответствующих размеров.

Условие. Определить периметр треугольника ABC, с медианой AK = 25 мм, построенного по следующим исходным данным:

□ AK = 20 мм, BK = 16 мм;

□ ВС = 35 мм, высота АР =15 мм;

□ ВС = 32 мм, АВ = 16 мм.

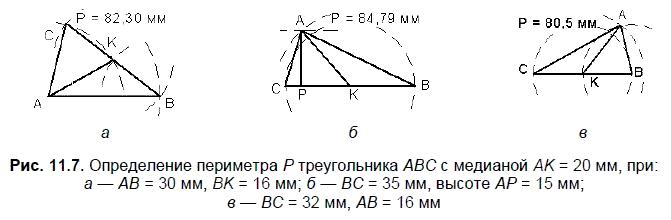
Решение. На рис. 11.7 частично показаны вспомогательные окружности, с помощью которых определяются вершины искомых треугольников. Рассмотрим последовательности построений:

□ а — отрезок АВ; окружности с центром А радиуса 20 мм и с центром В радиуса 16 мм; с центром K радиуса 16 мм;

□ б — отрезок СВ; окружности с центром K радиуса 17,5 мм и радиуса 20 мм;

□ в — окружности с центром K радиуса 16 мм и радиуса 20 мм; с центром В радиуса 16 мм.

Условие. Две окружности, диаметры которых равны 30 и 20 мм, имеют внутреннее касание в точке А (рис. 11.8, а). Найти диаметр третьей окружности, касающейся двух и их общего диаметра.

Решение. Вначале необходимо построить две окружности заданных диаметров и отрезок, проходящий через их центры. Затем необходимо вызвать команду Окружность, касательная к трем кривым, построить третью окружность и измерить ее диаметр.

Условие. В прямоугольном треугольнике ABC, гипотенуза АВ которого равна 30 мм, проведены медианы АМ и BN (рис. 11.8, б). Известно, около четырехугольника ABMN можно описать окружность. Найти ее диаметр.

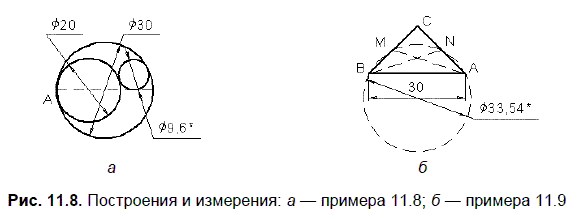
Решение. Вначале строится отрезок АВ заданной длины. Затем из точек А и В проводятся два отрезка под углами 135° и 45° и с использованием команды Выровнять по границе определяется точка С. При включенной привязке Середина несложно провести медианы АМ и BN. На заключительном этапе проводится Окружность по трем точкам и определяется ее диаметр.

Условие. Точка K лежит на продолжении стороны AD ромба ADCD за точку D, Е — точка пересечения АС и BK (рис. 11.9), AK = 70 мм, точки А, В и Е лежат на окружности диаметра 60 мм, центр которой принадлежит отрезку AK. Найти длину отрезка BK.