Н. — Мы, следовательно, имеем (4·6252·25)/(2·3) = 6 500 000гц.
Ничего себе! Видеочастота превышает шесть миллионов!
Л. — Реально передаются частоты до 6 Мгц. И ты заметь, что максимальная частота пропорциональна квадрату числа строк. Таким образом, если перейти от 625 строк к разложению на 1 000 строк, то видеочастота достигнет почти 17 Мгц,
Н. — Ты меня этим совершенно ошеломил.

Л. — Ты по-прежнему упорствуешь в своем намерении уделить телевидению «небольшое местечко» в диапазоне средних волн?
Н. — Он простирается от 200 до 600 м, следовательно, от 1500 000 до 500 000 гц. Весь интервал равен 1000 000 гц. В то же время телевизионная передача с боковыми полосами растягивается на 12 000 000 гц. Следовательно, она в 12 раз больше общей протяженности средневолнового диапазона. Решительно слон не умещается в раковине улитки.
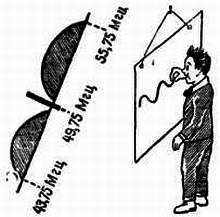
Л. — Очень приятно это слышать. Ты теперь понимаешь, почему необходимо прибегать к метровым волнам, чтобы передать модуляцию видеочастотой. Например, на частоте 49,75 Мгц боковые полосы будут ограничены следующими пределами:
49 750 000 — 6 000 000 = 43 750 000 гц
и
49 750 000 + 6 000 000 = 55 750 000 гц,
что вполне приемлемо.
Н. — Нужно ли, по правде говоря, так далеко забираться? Нельзя ли использовать, например, частоту 12 Мгц, т. е. 25 м, что позволит уместить модуляцию между
12 000 000 — 6 000 000 = 6 000 000 гц
и
12 000 000 + 6 000 000 = 18 000 000 гц?
Л. — Пойми, что длины волн, соответствующие этим частотам, составляют 50 и 16,5 м. Ты, стало быть, хочешь занять весь диапазон коротких волн между 16,5 и 50 м только одной телевизионной передачей?
Н. — Я признаю, что это было бы неразумно.
Л. — Существует правило, согласно которому высокая частота не может быть одного порядка с модулирующей частотой. Чтобы модуляция производилась без искажений, нужно, чтобы несущая частота была во много раз выше частоты модуляции.
Н. — Почему же?
Л. — Потому, что без этого модулирования волна не сможет точно воспроизвести модулирующее напряжение. Взгляни на синусоиду, которая здесь нарисована (рис. 6).
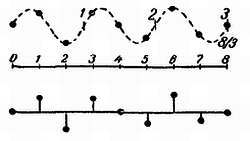
Рис. 6. При передаче синусоидального сигнала (представленного вверху синусоидой) с помощью несущей частоты, восемь периодов которой приходятся на три периода сигнала, передаваемому сигналу соответствуют редко расположенные значения (представленные внизу), которые не позволяют восстановить форму сигнала.
Допустим, что что сигнал, который нужно передать. Если частота несущей превышает частоту этого сигнала, например, в отношении 8/3, то мы передадим соответствующие мгновенные значения только с очень большими интервалами и получим ряд отдельных значений, по которым будет невозможно при всем желании воспроизвести закон синусоидального изменения. Но возьми несущую волну с частотой, в 8 раз большей частоты сигнала (рис. 7). Последовательность переданных величин позволит легко воспроизвести форму модулирующего напряжения.
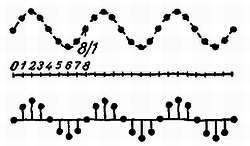
Рис. 7. Если на каждый период синусоидального сигнала приходится восемь периодов несущей частоты, то при этом передается достаточно большое количество мгновенных значении сигнала, чтобы он мог быть надлежащий образом воспроизведен.
Н. — Это все равно, что растр газетных фотографических клише. Если растр слишком крупный, детали клише пропадают.
Л. — Это неплохое сравнение.

Н. — Резюмирую все, о чем мы сегодня говорили. Передача изображений требует сигналов, занимающих очень широкую полосу частот. Эти сигналы могут передаваться только несущими волнами очень высокой частоты в диапазоне метровых волн. Распространяясь по прямой линии, они имеют радиус действия, ограниченный видимым горизонтом. Отсюда следует, что у моего дядюшки не будет телевидения.
Л. — Я страшно огорчен за него. Но что касается тебя, то ты узнал некоторое количество полезных сведений…
Н. — …которые мне показались сначала дьявольски сложными, но которые, по сути дела, может быть, и очень просты.

Беседа вторая
ПУТЕШЕСТВИЕ В ПРОШЛОЕ
Чтобы понять действие аппаратуры современного телевидения, нет необходимости изучать всю историю этой области техники. Однако изучение способов разложения изображения значительно облегчится в результате предварительного изложения классической «механической» системы телевидения, предложенной Нипковым.
Незнайкин легко поймет метод, который впервые дал возможность передачи движущихся изображений на расстояние. В ходе этой беседы Любознайкин, следовательно, затронет следующие вопросы: диск Нипкова; разложение изображения; чересстрочная развертка; фотоэлемент; передатчик изображений; синхронизм; приемник с неоновой лампой; недостатки механических систем телевидения.

Любознайкин. — Боже мой! Что с тобой, Незнайкин, почему ты кружишься вокруг себя? Ты упражняешься в ремесле вертящегося дервиша?
Незнайкин. — Да вовсе нет! Я просто пробую читать так, чтобы, дойдя до конца строчки, не переводить взгляда обратно, налево, к началу следующей строчки.
Л. — А зачем это?
Н. — Потому, что я думаю о развертке изображения в телевидении, о котором мы говорили в последний раз. Ты мне объяснил, что последовательное разложение элементов производится, как чтение книги: строчка за строчкой. Принимая во внимание огромную скорость, с которой должно производиться это чтение, я хотел бы избежать потери времени, вызванной необходимостью возвращения к началу строк. Вот почему, пробежав, поворачиваясь, одну строку, я продолжаю быстрое вращательное движение вокруг самого себя, чтобы после каждого оборота мой взгляд снова попал на начало строк.
Л. — Не думаю, чтобы таким образом ты выгадал время. Самое большее — ты заработаешь на этом головокружение… Но этот способ развертки, который можно назвать «без обратного хода по строкам», характерен для большей части механических способов анализа.
Н. — Неплохо, если бы ты об этом поговорил. Потому что все, что ты до сих пор объяснял, довольно абстрактно. Очень мило сказать, что производят последовательную развертку элементов изображения. Но как это происходит в действительности?
Л. — Я предпочел бы не описывать тебе механические способы, потому что они уступили место электронным. Но, может быть, ты лучше поймешь электронные методы, если я тебе расскажу об одном из самых простых и самых старинных устройств — диске Нипкова.