Если же вы все-таки рискнете самостоятельно выяснять, какая камера лучше снимает, то самая подробная страница в Рунете на эту тему здесь. Но будьте осторожны — выбирать камеру с помощью тестов можно до бесконечности, поскольку идеала нет и не будет никогда.

Как движется вода под действием силы тяжести? Как она обтекает попадающиеся ей на пути препятствия? Как устроены воздушные потоки вокруг самолета? Ответы на эти вопросы в общем виде физикам неизвестны, и упираются эти ответы в решение уравнений Навье-Стокса, о которых и пойдет рассказ.

«Проблема на миллион», о которой мы поговорим сегодня, имеет достаточно простую, но не слишком привлекательную математическую формулировку: задача существования, гладкости и единственности некоторой системы дифференциальных уравнений… бррр, это вам не числа от одного до бесконечности складывать[Впрочем, это дело вкуса. Свой вкус никому навязывать не хочу, но интуиция подсказывает, что среди читателей «Компьютерры» любителей дискретной математики должно быть больше, чем любителей матфизики]. Зато ее физический смысл более чем прозрачен, а применения обширны и очевидны.

Итак, откуда же есть пошли уравнения Навье-Стокса? Они описывают поведение жидкостей и газов. Да-да, оказывается, физики, создающие теории двадцати-с-лишним-мерного пространства суперструн, решающие загадки черных дыр и полным ходом движущиеся к построению квантового компьютера, до сих пор не могут описать поведение самой обычной воды. Все уравнения вполне естественны и, по большому счету, очевидны из общепринятой физической модели несжимаемой жидкости. Первое из уравнений — это второй закон Ньютона, F=ma. Правда, в F, кроме внешней силы f=(f(i), i=1...n) (общая постановка задачи формулируется в n-мерном пространстве, но интересный случай, конечно, тот, в котором n равно трем[Вспоминается известный анекдот про математика, который шел по улице и заметил вывеску: «Камерный оркестр». «Интересно…» — подумал математик и зашел. Через минуту вышел разочарованный: «Тривиальный случай… ка равно трем». В нашей задаче ка, равное трем, — отнюдь не тривиальный случай]), должны войти также силы, отвечающие за давление p и трение внутри жидкости. Итого получается:

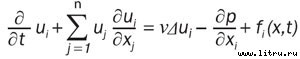
где u(x,t)=ui(x,t)— неизвестный вектор скорости, x — n-мерный вектор координат, t — время, а n — коэффициент вязкости. Второе уравнение говорит, что жидкость несжимаема. На математическом языке это выглядит так:

div u = 0.

Кроме того, разумеется, уравнения должны быть снабжены начальными условиями, причем, чтобы оставаться в рамках разумных физических моделей, как начальный вектор, так и сила f (точнее, их производные) должны достаточно быстро уменьшаться по мере удаления от нуля координат к бесконечности, а вся система должна иметь ограниченную энергию:

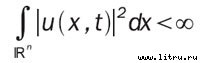
Свои имена уравнениям дали французский инженер Клод-Луи Навье (Claude-Louis Navier), выдающийся мостостроитель, разработавший первую в мире теорию подвесных мостов, и Джордж Габриэль Стокс (George Gabriel Stokes), научные заслуги которого в основном относятся к математической физике и дифференциальной геометрии. Кстати, Стокс дал имя британской единице вязкости.

Неудивительно, что эти уравнения долгое время привлекали внимание математиков всего мира. И здесь есть серьезные причины для гордости за отечественную науку: весомый вклад в развитие теории уравнений Навье-Стокса внесла Ольга Александровна Ладыженская, одна из замечательных представителей петербургской математической школы. Главным результатом Ладыженской в этой области было полное решение проблемы в двумерном случае: Ольга Александровна доказала однозначную разрешимость задачи. В трехмерном случае она получила частичные результаты: доказала однозначную разрешимость уравнений на конечном промежутке времени, а также решила общую задачу в предположении малости так называемого числа Рейнольдса (этот параметр задает соотношение между инерцией и вязкостью; при больших значениях числа Рейнольдса поток становится турбулентным). А вот вопрос о единственности так называемого слабого решения Хопфа, которое существует для бесконечного промежутка, до сих пор остается открытым — и за ответ на него решение Clay Mathematical Institute готов заплатить миллион долларов.

Вклад Ладыженской в математику, разумеется, не ограничивался решением двумерных уравнений Навье-Стокса: достаточно сказать, что работы, выполненные ею в сотрудничестве со своей ученицей Ниной Николаевной Уральцевой[Мне посчастливилось слушать курс матфизики у Нины Николаевны и лично знать Ольгу Александровну (благодаря поддержке которой я и оказался в СПбГУ); правда, уроки на пользу не пошли, и при выборе научного пути матфизике я предпочел алгебру и информатику], фактически закрыли цикл исследований по 19-й и 20-й проблемам Гильберта. Эти фантастические достижения навсегда вписали Ольгу Александровну в историю математики. Но, на мой взгляд, не менее фантастическим является ее научное долголетие. До последних дней жизни (это не штамп и не преувеличение) Ольга Александровна активно занималась научной деятельностью, редактировала многочисленные научные сборники, участвовала в конференциях — и ушла из жизни 12 января 2004 года, немного не дожив до своего восемьдесят второго дня рождения…

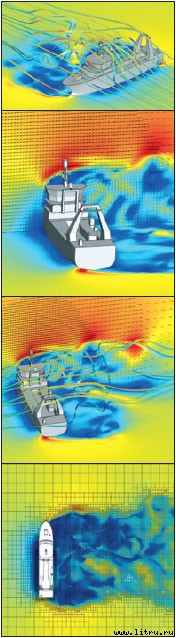
Но вернемся к уравнениям Навье-Стокса. Аналитическому решению они не поддаются, однако проектировать подводные лодки и особенно самолеты (разумеется, движение воздуха описывается теми же уравнениями, только вязкость у воздуха гораздо меньше, чем у воды, — а, значит, турбулентность больше, и решать уравнения методом Ладыженской не получается) все-таки нужно. Что делать? Ответ прост и для физиков традиционен: решать уравнения приближенно. И здесь, конечно, компьютерные технологии пришлись ко двору. Возник целый раздел на грани матфизики и computer science — вычислительная динамика жидкостей и газов (computational fluid dynamics, CFD).

Wikipedia предлагает целую коллекцию ссылок на программные продукты (как коммерческие, так и свободные), реализующие различные задачи вычислительной динамики. Примечательно, что один из самых успешных проектов — система OpenFOaM (Open Field Operation and Manipulation) — начинал свой путь как коммерческий, закрытый продукт, а затем был переведен разработчиками под GPL. Наверное, его и можно порекомендовать желающим всерьез заняться этим направлением — для него написано множество расширений и библиотек, и благодаря открытой архитектуре проекта и активному сообществу разработчиков количество этих расширений увеличивается. А красивые картинки, например, получаются из Gerris Flow Solver, хотя, конечно, глаз вряд ли способен насладиться рисованными векторными полями так же, как видом трехмерной, играющей на солнце всеми красками радуги жидкости. Для всевозможных пакетов трехмерного моделирования написано множество CFD-плагинов, позволяющих добавлять в трехмерную сцену «физически точные» картины различных течений. Обычно они стоят немалых денег (например, RealFlow, плагин для 3DS MAX, продается по сверхнизкой цене всего лишь в 1080 долларов), но в России, как известно, цена софта — штука весьма и весьма условная…

Итак, подводим итоги. Уравнения Навье-Стокса — центральная проблема современной математической физики. Существуют целые конференции, посвященные исключительно этим уравнениям (например, конференция в Киото, запланированная на 2006 год, или петербургская конференция, прошедшая в 2002 году), и миллион долларов за их решение назначен не зря. Однако практические применения уравнений не очень сильно страдают от проблем с аналитичностью или единственностью решений. Самолеты, конечно, иногда падают, а подводные лодки тонут, но обычно это происходит по причинам, весьма далеким от уравнений Навье-Стокса — и, сдается мне, устранить эти причины куда труднее, чем решить какую бы то ни было задачу на миллион…