Другая важная физическая величина, колеблющаяся вместе со смещением и скоростью частицы,- это избыточное давление, называемое также звуковым. Звуковое колебание воздуха состоит в периодическом чередовании сжатия и разрежения в каждой точке среды. Давление воздуха в любом месте то больше, то меньше давления, которое было при отсутствии звука. Этот избыток (или недостаток) давления и называется звуковым. Звуковое давление составляет совсем небольшую долю нормального давления воздуха. Для нашего примера - громкий разговор - амплитуда звукового давления будет равна примерно миллионной доле атмосферы. Звуковое давление прямо пропорционально скорости колебания частицы, причем отношение этих физических величин зависит только от свойств среды. Например, звуковому давлению в воздухе в 1 дин/см2 соответствует скорость колебания 0,025 см/с.

Рис. 6.9
Струна, колеблющаяся по закону синуса, приводит и частицы воздуха в гармоническое колебание. Шумы и музыкальные аккорды приводят к значительно более сложной картине. На рис. 6.9 показана запись звуковых колебаний, а именно звукового давления в зависимости от времени. Эта кривая мало похожа на синусоиду. Оказывается, однако, что любое сколь угодно сложное колебание может быть представлено как результат наложения одной на другую большого числа синусоид с разными амплитудами и частотами. Эти простые колебания, как говорят, составляют спектр сложного колебания. Для простого примера такое сложение колебаний показано на рис. 6.10.

Рис. 6.10
Если бы звук распространялся мгновенно, то все частицы воздуха колебались бы, как одна. Но звук распространяется не мгновенно, и объемы воздуха, лежащие на линии распространения, приходят в движение по очереди, как бы подхватываются волной, идущей от источника. Так же точно щепка лежит спокойно на воде до тех пор, пока круговые водяные волны от брошенного камешка не подхватят ее и не приведут в колебание.
Остановим наше внимание на одной колеблющейся частице и сравним ее поведение с движением других частиц, лежащих на той же линии распространения звука. Соседняя частица придет в колебание немного позже, следующая - еще позже. Запаздывание будет нарастать, пока, наконец, мы не встретимся с частицей, отставшей на целый период и поэтому колеблющейся в такт с исходной. Так отставший на целый круг неудачный бегун может пройти линию финиша одновременно с лидером. На каком же расстоянии встретим мы точку, колеблющуюся в такт с исходной? Нетрудно сообразить, что это расстояние ? равно произведению скорости распространения звука с на период колебания Т. Расстояние ? называется длиной волны:
? = cT.
Через промежутки ? мы будем встречать колеблющиеся в такт точки. Точки, находящиеся на расстоянии ?/2, будут совершать движение одна по отношению к другой, как предмет, колеблющийся перпендикулярно к зеркалу, по отношению к своему изображению.
Если изобразить смещение (или скорость, или звуковое давление) всех точек, лежащих на линии распространения гармонического звука, то получится опять синусоида.
Не следует путать графики волнового движения и колебаний. Рис. 6.11 и 6.12 очень похожи, но на первом по горизонтальной оси отложено расстояние, а на втором - время. Один рисунок представляет собой временную развертку колебания, а другой - мгновенную "фотографию" волны. Из сопоставления этих рисунков видно, что длина волны может быть названа также ее пространственным периодом: роль Т во времени играет в пространстве величина ?.

Рис. 6.11
На рисунке звуковой волны смещения частицы отложены по вертикали, а направлением распространения волны, вдоль которого отсчитывается расстояние, является горизонталь. Это может навести на неверную мысль, что частицы смещаются перпендикулярно к направлению распространения волны. В действительности частицы воздуха всегда колеблются вдоль направления распространения звука. Такая волна называется продольной.

Рис. 6.12
Свет распространяется несравненно быстрее, чем звук,- практически мгновенно. Гром и молния происходят в один и тот же момент, но молнию мы видим в момент ее возникновения, а звук грома доходит до нас со скоростью примерно один километр за три секунды (скорость звука в воздухе составляет 330 м/с). Значит когда слышен гром, опасность удара молнии уже миновала.
Зная скорость распространения звука, обычно можно определить, как далеко проходит гроза. Если от момента вспышки молнии до раската грома прошло 12 с, значит, гроза от нас за 4 км.
Скорость звука в газах примерно равна средней скорости движения молекул газа. Она также зависит от плотности газа и пропорциональна корню квадратному из абсолютной температуры. Жидкости проводят звук быстрее, чем газы. В воде звук распространяется со скоростью 1450 м/с, т. е. в 4,5 раза быстрее, чем в воздухе. Еще больше скорость звука в твердых телах, например, в железе - около 6000 м/с.
Когда звук переходит из одной среды в другую, меняется скорость его распространения. Но одновременно происходит и другое интересное явление - частичное отражение звука от границы между двумя средами. Какая доля звука отразится - это зависит главным образом от соотношения плотностей. В случае падения звука из воздуха на твердые или жидкие поверхности или, наоборот, из плотных сред в воздух звук отражается почти полностью. Когда звук попадает в воду из воздуха или, наоборот, из воды в воздух, то во вторую среду проходит всего лишь 1/1000 силы звука. Если обе среды плотные, то отношение между проходящим и отраженным звуком может быть и невелико. Например, из воды в сталь или из стали в воду пройдет 13%, а отразится 87% звука.
Явление отражения звука широко применяется в навигации. На нем основано устройство прибора для измерения глубины - эхолота. У одного борта корабля под водой помещают источник звука (рис. 6.13). Отрывистый звук создает звуковые лучи, которые проберутся сквозь водяную толщу ко дну моря или реки, отразятся от дна, и часть звука вернется на корабль, где ее улавливают чувствительные приборы. Точные часы укажут, сколько времени понадобилось звуку на это путешествие. Скорость звука в воде известна, и простым вычислением можно получить точные сведения о глубине.

Рис. 6.13
Направляя звук не вниз, а вперед или в стороны, можно при его помощи определить, нет ли около корабля опасных подводных скал или глубоко погруженных в воду айсбергов. Все частицы воздуха, окружающего звучащее тело, находятся в состоянии колебания. Как мы выяснили в книге 1, колеблющаяся по закону синуса материальная точка обладает определенной и неизменной полной энергией.
Когда колеблющаяся точка проходит положение равновесия, скорость ее максимальна. Так как смещенные точки в это мгновение равняется нулю, то вся энергия сводится к кинетической:
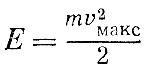
Следовательно, полная энергия пропорциональна квадрату амплитудного значения скорости колебания.
Это верно и для частиц воздуха, колеблющихся в звуковой волне. Однако частица воздуха - это нечто неопределенное. Поэтому энергию звука относят к единице объема. Эту величину можно назвать плотностью звуковой энергии.
Так как масса единицы объема есть плотность ?, то плотность звуковой энергии

Мы говорили выше еще об одной важной физической величине, совершающей колебания по закону синуса с той же частотой, что и скорость. Это - звуковое или избыточное давление. Так как эти величины пропорциональны, то можно сказать, что плотность энергии пропорциональна квадрату амплитудного значения звукового давления.