Попробуйте задачу на сложение пятизначных чисел, округляя их до ближайшей сотни.

Благодаря округлению до ближайшей сотни погрешность нашего ответа всегда будет меньше 100. Если ответ больше 10 000, приближенная оценка будет в пределах 1 % от точного ответа.

Теперь попробуем что-нибудь посложнее.

Если вы округлите до ближайшего миллиона, то получите ответ в 31 миллион, что примерно на 285 000 меньше истинного значения. Неплохо, конечно, но вы можете улучшить ответ, округляя до ближайших ста тысяч, как показано в последнем столбце. В этом случае приближенная оценка снова будет в пределах находиться 1 % от точного ответа. Если вы научитесь находить точные ответы для таких задач с меньшими числами, то сможете приблизительно оценить ответ в любой задаче.

Приближенная оценка в супермаркете

Рассмотрим пример из реальной жизни. Придя в магазин, вы когда-нибудь интересовались общей суммой покупки до того, как кассир пробил чек? Для оценки общей суммы я использую технику округления цен до ближайших 50 центов. Например, пока кассир складывает числа, показанные слева, я мысленно суммирую числа, показанные справа.

1,39 1,50

0,87 1,00

2,46 2,50

0,61 0,50

3,29 3,50

2,99 3,00

0,20 0,00

1,17 1,00

0,65 0,50

2,93 3,00

3,19 3,00

^____________

19,75 19,50

Моя итоговая цена, как правило, колеблется в пределах одного доллара от точного значения.

Способ получения приближенной оценки при вычитании такой же, как и при сложении: округляем до ближайшей тысячи или сотни (последнее предпочтительнее).

Как видите, округление до ближайшей тысячи делает ответ не совсем корректным. Благодаря округлению второй цифры (до сотен в нашем примере) погрешность обычно колеблется в пределах 3 %. В данной задаче приближенное решение отклоняется от истинного ответа лишь на 52, поэтому относительная погрешность составляет 2 %. Если округлять третью цифру, то относительная погрешность обычно будет меньше 1 %.

Например:

Путем округления третьей цифры вместо второй можно значительно улучшить точность оценки.

Первый и самый важный шаг расчета приближенного ответа для задачи на деление — это определить величину частного.

Следующий шаг — округление большего из чисел до ближайшей тысячи, то есть замена 57 867 на 58 000. Деление 58 на 6 дает 9 с остатком. Но самый важный элемент решения данной задачи — это поиск местоположения цифры 9.

Например, в результате умножения 6 х 90 получается 540, тогда как 6 х 900 = 5400. Оба варианта дают слишком малые числа. Но 6 х 9000 = 54 000, что достаточно близко к делимому. Это говорит о том, что ответ будет 9 000 плюс «что-то». Можно прикинуть это «что-то», сначала отняв 58–54 = 4. В этом случае вам нужно снести 0 и разделить 40 на 6 и т. д. Но если вы внимательны, то поймете, что деление 4 на 6 дает 4/6 = 2/3, что приблизительно равно 0,667. Поскольку ваш ответ «9 000 плюс что-то», теперь можно сказать «9 667». В действительности точный ответ будет 9 645.

Чертовски близко!

Деление чисел на таком уровне кажется довольно простым. Но как быть с большими задачами на деление? Скажем, мы хотим посчитать, забавы ради, сколько зарабатывает профессиональный спортсмен в день, если его зарплата за год составляет 5 000 000 долларов.

Первым делом нужно оценить примерный ответ. Этот игрок зарабатывает каждый день тысячи? Ну, если 365 х 1000 = 365 000, то получается слишком мало.

Или десятки тысяч? Ну, 365 х 10 000 = 3 650 000. Это уже больше похоже на правду. Для получения приближенной оценки разделите первые две цифры (50 на 36), и у вас получится 1 и 14/36, или 1 и 7/18. Так как 70 — это примерно 4 раза по 18, выходит, что спортсмен зарабатывает около 14 000 долларов в день. Точный ответ — 13 698,63 доллара. Неплохая точность. (И неплохая зарплата!)

А вот астрономический расчет. Сколько секунд необходимо свету, чтобы долететь от Солнца до Земли? Свет перемещается со скоростью 186 282 мили в секунду, а Солнце находится на расстоянии (в среднем) 92 960 130 миль от Земли. Я сомневаюсь, что вы очень хотите решить эту задачку вручную.

К счастью, приближенную оценку ответа достаточно легко получить. Сначала упростим задачу.

Теперь разделим 930 на 186, что даст нам 5 без остатка. Потом добавим два 0, которые забрали у 93 000, и получим 500 секунд. Точный ответ — 499,02 секунды. Этот пример показывает, что приближенная оценка может заслуживать большого уважения.

Для приблизительной оценки ответов в задачах на умножение используются примерно те же приемы, что и описанные выше. Например:

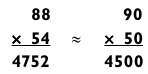
Округление до ближайшего кратного 10 значительно упрощает задачу, но ответ все еще на 252 меньше истинного (погрешность около 5 %). Можно улучшить ситуацию, округлив оба числа на одинаковую величину в разных направлениях.

Так, если округлить 88 до 90, то 54 следует уменьшить на 2.

Итак, вместо задачи на умножение типа «2 на 2» теперь мы имеем дело с умножением типа «2 на 1», что не должно быть для вас сложным. В данном случае приближенная оценка отклоняется от истинного значения всего на 1,5 %.

Если приближенный ответ для задачи на умножение получен путем округления большего числа в большую сторону и меньшего в меньшую, то он будет несколько занижен. Если округлить большее число в меньшую сторону, а меньшее в большую (тогда, возможно, числа станут достаточно близкими), приближенный ответ получится слегка завышенным.

Чем больше величина, на которую вы округляете в ту или иную сторону, тем большее отклонение будет иметь приближенная оценка. Например:

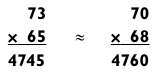
Поскольку после округления числа стали близки друг к другу, приближенная оценка получилась слегка завышенной.

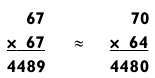
Так как перемножаемые числа не близки друг к другу, приближенная оценка ответа занижена, но ненамного. Нетрудно заметить, что метод приближенной оценки весьма эффективно работает для примеров на умножение. Кроме того, обратите внимание, что данный пример — это задача на возведение в квадрат 67², и наше приближение — всего лишь первый шаг в технике возведения в квадрат. Рассмотрим еще один пример.