Займемся этим теперь. Ясно, что мы не можем, вообще говоря, определить положение материальной частицы с помощью материальной точки, а траекторию ее движения — с помощью математической линии, поскольку в квантовом мире все объекты расплываются. Нам необходимо обратиться к другим методам описания, дающим, так сказать, «плотность размазни» в различных точках пространства. Математически это означает, что мы используем непрерывные функции (такие как, например, в гидромеханике), а физически требует, чтобы при описании квантового мира мы употребляли такие обороты речи, как «этот объект в основном находится здесь, частично там и даже вон там» или «эта монета на 75% находится в моем кармане и на 25% — в вашем». Я понимаю, что такие утверждения кажутся вам дикими, но в нашей повседневной жизни из-за малости квантовой постоянной в них нет надобности. Но если вы вознамеритесь изучать атомную физику, то я настоятельно рекомендую вам предварительно привыкнуть к такого рода выражениям.

Считаю своим долгом предостеречь вас от ошибочного представления о том, будто функция, описывающая «плотность пребывания» объекта в различных точках пространства, обладает физической реальностью в нашем обычном трехмерном пространстве. Действительно, если мы описываем поведение, например, двух частиц, то нам необходимо ответить на вопрос, находится ли одна частица в одном месте и, одновременно, вторая частица в другом месте. Для этого нам необходима функция шести переменных (координат двух частиц), которую невозможно «локализовать» в трехмерном пространстве. Для описания более сложных систем нам понадобились бы функции еще большего числа переменных. В этом смысле «квантово-механическая функция» аналогична «потенциальной функции», или «потенциалу», системы частиц в классической механике или «энтропии» системы в статистической механике: она только описывает движение и позволяет нам предсказывать результат любого конкретного движения при данных условиях. Физическая реальность остается за частицами, движение которых мы описываем.

Функция, которая описывает, какая «доля» частицы или системы частиц присутствует в различных местах пространства, требует специального математического обозначения. Следуя Эрвину Шредингеру, который первым написал уравнение, определяющее поведение такой функции, ее стали обозначать

.

Я не стану сейчас вдаваться в детали математического вывода фундаментального уравнения Шредингера. Хочу лишь обратить ваше внимание на требования, которые привели к его выводу. Самое важное из этих требований весьма необычно: уравнение должно быть записано в таком виде, чтобы функция, описывающая движение материальных частиц, обладала всеми свойствами волны.

На необходимость наделить движение материальных частиц волновыми свойствами впервые указал французский физик Луи де Бройль на основе своих теоретических исследований строения атома. В последующие годы волновые свойства движения материальных частиц были надежно подтверждены многочисленными экспериментами, продемонстрировавшими такие явления, как дифракция пучка электронов при прохождении через малое отверстие и интерференционные явления, происходящие даже с такими сравнительно большими и сложными частицами, как молекулы.

Экспериментально установленные волновые свойства материальных частиц были совершенно непонятны с точки зрения классических представлений о движении, и де Бройль был вынужден принять весьма необычную (чтобы не сказать неестественную) точку зрения: по де Бройлю, все частицы «сопровождаются» определенными волнами, которые, так сказать, «направляют» их движения.

Но как только мы отказываемся от классических понятий и переходим к описанию движения с помощью непрерывных функций, требование о волновом характере становится гораздо более понятным. Оно просто утверждает, что распространение нашей

—функции аналогично (например) нераспространению тепла сквозь стенку, нагреваемую с одной стороны, а распространению сквозь ту же самую стенку механической деформации (звука). Математически это означает, что мы ищем уравнение определенного (а не ограниченного) вида. Это фундаментальное условие вместе с дополнительным требованием, чтобы наши уравнения, если их применять к частицам большой массы, переходили в уравнения классической механики, поскольку квантовые эффекты для таких частиц становятся пренебрежимо слабыми, практически сводят проблему вывода уравнения к чисто математическому упражнению.

Если вас интересует, как выглядит окончательный ответ — фундаментальное уравнение Шредингера, то я могу выписать его. Вот оно:

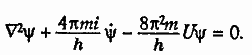
(7)

Здесь U означает потенциал сил, действующих на нашу частицу (с массой m), и порождает определенное решение задачи о движении частицы при любом заданном распределении силы. «Волновое уравнение Шредингера» (так принято называть выведенное Шредингером фундаментальное уравнение) позволило физикам в последующие сорок лет его существования построить наиболее полную и логически непротиворечивую картину явлений, происходящих в мире атомов.

Некоторые из вас, должно быть, удивляются, почему я до сих пор ни разу не употребил слово «матрица», которое часто приходится слышать в связи с квантовой теорией. Должен признаться, что лично я питаю сильную неприязнь к матрицам и предпочитаю обходиться без них. Но чтобы не оставлять вас в абсолютном неведении относительно этого математического аппарата квантовой теории, я скажу о матрицах несколько слов. Как вы уже знаете, движение частицы или сложной механической системы всегда можно описать с помощью некоторых непрерывных волновых функций. Эти функции часто бывают очень сложными и представимы в виде набора из некоторого числа более простых колебаний (так называемых «собственных функций») подобно тому, как сложный звук можно составить из некоторого числа простых гармонических тонов. Сложное движение можно описывать, задавая амплитуды его различных компонент. Поскольку число компонент (обертонов) бесконечно, мы выписываем бесконечную таблицу амплитуд вида

(8)

Над такими таблицами можно производить математические операции по сравнительно простым правилам. Каждая такая таблица и называется «матрицей», и некоторые физики вместо того, чтобы иметь дело непосредственно с волновыми функциями, предпочитают оперировать с матрицами. Такая «матричная механика», как ее иногда называют, представляет собой не более чем математическую модификацию обычной «волновой механики». В наших лекциях, посвященных главным образом принципиальным вопросам, было бы излишне входить в эти проблемы более подробно.

Очень жаль, что недостаток времени не позволяет мне рассказать вам о дальнейшем прогрессе квантовой теории в связи с теорией относительности. Эта глава в развитии квантовой теории, связанная главным образом с работами британского физика Поля Адриена Мориса Дирака, приводит ко многим интереснейшим проблемам и стала основой некоторых чрезвычайно важных экспериментальных открытий. Возможно, когда-нибудь в другой раз я еще вернусь к этим проблемам, а пока я должен остановиться. Надеюсь, что прочитанная мной серия лекций позволила вам составить более ясное представление о современной концепции физического мира и пробудила в вас интерес к дальнейшим научным занятиям.

На следующее утро мистер Томпкинс еще нежился в постели, как вдруг почувствовал, что в комнате есть еще кто-то. Оглядевшись вокруг, он обнаружил своего старого друга профессора. Тот сидел в кресле, уткнувшись в расстеленную на коленях карту и внимательно изучал ее.

— Так вы со мной? — спросил профессор, поднимая голову.