Общая теория относительности А.Эйнштейна предсказала своеобразный и неожиданный эффект: не только планеты вращаются вокруг Солнца, но и эллипсы, которые они описывают, должны очень медленно вращаться относительно солнца. Это вращение тем больше, чем ближе планета к Солнцу. Для всех планет, кроме Меркурия, оно настолько мало, что не может быть уловлено. Эллипс Меркурия, ближайшей к Солнцу планеты, осуществляет полное вращение в 3 млн. лет, что удаётся обнаружить. И вращение этого эллипса действительно было открыто астрономами, причём задолго до Эйнштейна. Никакого объяснения такому вращению не находилось. Теория относительности не опиралась при своей формулировке на данные об орбите Меркурия. Поэтому когда из её гравитационных уравнений было выведено оказавшееся верным заключение о вращении эллипса Меркурия, это справедливо было расценено как важное свидетельство в пользу теории относительности.

Подтверждение неожиданных предсказаний, сделанных на основе какого-то положения, существенно повышает его правдоподобность.

Неожиданное предсказание — это предсказание, связанное с риском, что оно не подтвердится. Чем более рискованно предсказание, выдвигаемое на основе какой-то теории, тем больший вклад в её обоснование вносит подтверждение этого предсказания.

Типичным примером здесь может служить предсказание теории гравитации Эйнштейна, что тяжёлые массы (такие, как Солнце) должны притягивать свет точно так же, как они притягивают материальные тела. Вычисления, произведённые на основе этой теории, показывали, что свет далёкой фиксированной звезды, видимой вблизи Солнца, достиг бы Земли по такому направлению, что звезда казалась бы смещённой в сторону от Солнца, иначе говоря, наблюдаемое положение звезды было бы сдвинуто в сторону от Солнца по сравнению с реальным положением. Этот эффект нельзя наблюдать в обычных условиях, поскольку близкие к Солнцу звезды совершенно теряются в его лучах. Их можно сфотографировать только во время затмения. Если затем те же самые звезды сфотографировать ночью, то можно измерить различия в их положении на обеих фотографиях и таким образом подтвердить предсказанный эффект. Экспедиция Эддингтона отправилась в Южное полушарие, где можно было наблюдать очередное солнечное затмение, и подтвердила, что звезды действительно меняют своё положение на фотографиях, сделанных днём и ночью. Это оказалось одним из наиболее важных свидетельств в пользу эйнштейновской теории гравитации.

Как бы ни было велико число подтверждающихся следствий и, какими бы неожиданными, интересными или важными они ни оказались, положение, из которого они выведены, все равно остаётся только вероятным. Никакие подтвердившиеся следствия не способны сделать его истинным. Даже самое простое утверждение в принципе не может быть доказано на основе одного подтверждения вытекающих из него следствий.

Это — центральный пункт всех рассуждений об эмпирическом подтверждении. Непосредственное наблюдение того, о чем говорится в утверждении, даёт уверенность в истинности последнего. Но область применения такого наблюдения является ограниченной. Подтверждение следствий — универсальный приём, применимый ко всем утверждениям. Однако приём индуктивный, только повышающий правдоподобие утверждения, но не делающий его достоверным.

Наряду с неполной индукцией принято выделять в качестве особого вида индуктивного умозаключения полную индукцию.

Её схема:

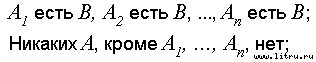
Следовательно, каждое А есть В.

Здесь в посылках о каждом из предметов, входящих в рассматриваемое множество, утверждается, что он имеет определённое свойство. В заключении говорится, что все предметы данного множества обладают этим свойством.

К примеру, учитель, читая список учеников какого-то класса, убеждается, что названные им ученики присутствуют. На этом основании учитель делает вывод, что присутствуют все ученики.

В полной индукции заключение с необходимостью, а не с некоторой вероятностью вытекает из посылок. Эта «индукция» является, таким образом, разновидностью дедуктивного умозаключения, хотя по внешней форме, по ходу мысли напоминает неполную индукцию.

К дедукции относится и так называемая математическая индукция, широко используемая в математике.

Умозаключение математической индукции слагается из двух посылок и заключения. Первая из посылок говорит, что рассматриваемое свойство присуще первому предмету рассматриваемого ряда. Вторая посылка утверждает, что если это свойство есть у произвольного предмета данного ряда, то оно есть и у непосредственно следующего за ним предмета. Заключение утверждает, что свойство присуще каждому предмету ряда.

Общая схема математической индукции:

A (1);

если А (k), то A (k + 1);

следовательно А (n).

Ни полная, ни математическая индукция не являются индуктивным умозаключением в собственном смысле этого слова. И та, и другая всегда дают истинные заключения из истинных посылок и только внешне напоминают индуктивные рассуждения.

Особую группу индуктивных умозаключений составляют рассуждения, с помощью которых обычно выявляются причинные связи.

Причинность — это определённое внутреннее отношение между явлениями, такая их связь, при которой всякий раз за одним следует другое. Причина — это явление, вызывающее к жизни другое явление. Результат действия причины — следствие.

В старину между стенами здания, подлежащего сносу, помещали прочный железный стержень и разводили под ним костёр. От нагревания стержень удлинялся, распирал стены, и они разваливались. Нагревание здесь причина, расширение стержня — её следствие.

Камень попадает в окно, и оно разлетается на осколки. Молния ударяет в дерево, оно раскалывается и обугливается. Извергается вулкан, пепел засыпает многометровым слоем город, и он гибнет. Начинается дождь, и на земле через некоторое время образуются лужи. Во всех этих случаях одно явление — причина — вызывает, порождает, производит и т.п. другое явление — своё следствие.

Что характерно для причинной связи? Чем она отличается от других возможных связей явлений?

Прежде всего, причина всегда предшествует во времени следствию. Сначала железо нагревается, а затем начинает расширяться. Окно раскалывается не до удара камня, а после него и т.д.

Основываясь на этом очевидном свойстве причинности, мы всегда ищем причину интересующего нас явления только среди тех явлений, которые предшествовали ему, и не обращаем внимания на все, что случилось позднее.

Далее, причинная связь необходима: всякий раз, когда есть причина, неизбежно наступает и следствие.

Вода при нормальном атмосферном давлении нагревается до 100°С, закипает и превращается в пар. Можно миллион раз нагревать воду до кипения, и она всегда будет переходить в пар. И если бы при миллион первом нагревании этого вдруг не произошло, мы должны были бы сказать, что между нагреванием воды и превращением её в пар нет причинной связи.

Названных характеристик причинности недостаточно, однако, для отличения её от связей других типов.

Наступлению каждого явления предшествует бесконечное множество других явлений. Но только одно из них может быть его причиной. Постоянное следование одного явления за другим не говорит ещё, что предшествующее — причина последующего. Ночь всегда предшествует утру, а за утром неизменно наступает день. Но ночь — не причина утра, а утро — не причина дня. Как предостерегает старая латинская пословица: «После этого не значит вследствие этого».

Причина всегда предшествует следствию, и следствие обязательно наступает в случае реализации причины. Но причина, сверх того, порождает и обусловливает следствие. В этом — ещё одна особенность причинной связи, отграничивающая её от всех других случаев постоянного следования одного явления за другим. Без этой особенности причинную связь невозможно охарактеризовать однозначно. Без неё нельзя, в частности, отличить причину от повода, т.е. события, которое непосредственно предшествует другому событию, делает возможным его появление, но не порождает и не определяет его.