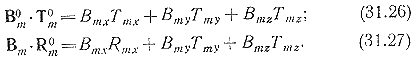Для определения компромиссного времени запуска применяется метод последовательных приближений. При этом производится варьирование ориентации плоскости промежуточной орбиты в инерциальном пространстве между векторами Т°1 и Т°2 таким образом, чтобы изменение плоскости движения приводило к получению одинакового веса в конце участка выведения для обеих возможностей запуска. Требуемая ориентация плоскости промежуточной орбиты соответствует компромиссному времени запуска и достигается путем варьирования N°1 и N°2 от исходных положений. Вектор N°2 варьируется посредством уменьшения времени запуска на величину ?Ts (измеряемую от времени второй возможности компланарного запуска), а вектор N°1 – путем увеличения времени запуска соответственно на ?TL—?Ts. Величина ?Tsизменяется до тех пор, пока веса в конце участков выведения для первой и второй возможностей запуска не станут равными. Для получения компромиссного времени запуска текущая величияа ?Ts вычитается затем из времени соответствующего второй возможности компланарного запуска.

Ошибка при определении компромиссного времени запуска описанным выше способом может достигать ~20 сек. Однако это время отвечает требованиям проведения итерационных расчетов, связанных с изменением плоскости движения при первой и второй возможностях запуска. После проведения этих расчетов полученные векторы цели, которые принадлежат гиперповерхности, соответствующей изменению плоскости движения, используются для расчета второго приближения компромиссного времени запуска. Нормальные к плоскости промежуточной орбиты векторы снова варьируются, чтобы уравнять веса на траектории полета к Луне. Использование скорректированного компромиссного времени запуска в программе моделирования активного участка показало достаточную точность процедуры уравнивания весов. Это приводило к незначительному расходу топлива на коррекцию среднего участка траектории, связанную с использованием времени запуска, отличающегося от запланированного.

Как следует из рис. 31.3, время запуска для задачи, относящейся к классу 2, определяется существенно проще. Времена запуска для первой и второй возможностей в случае в (рис. 31.3) не являются одинаковыми из-за прецессии орбиты к моменту наступления второй возможности старта. Однако это влияние незначительно и не затрагивает логики, которая используется при выборе траекторий класса 2. Анализ параметров прицеливания показывает, какой класс траекторий (1 или 2) должен использоваться. Когда установлено, что имеет место случай в, то участки вычислительной программы для случаев а и б обходятся. Вектор цели для второй возможности запуска и соответствующие параметры (гиперповерхность) вычисляются на основе времени старта при компланарном перелете. Время запуска для второй возможности используется при определении параметров прицеливания для первой возможности. Как указывалось выше, это время запуска не будет являться оптимальным для первой возможности, однако оно отличается от оптимального всего на несколько секунд.

Как отмечалось выше, лунными параметрами прицеливания (т. е. зависимыми переменными в схеме вычислений) являются радиус максимального сближения Rm и широта ?* в селеноцентрической системе координат. Однако эти переменные являются нелинейными по отношению к изменению независимых переменных. Определение широты ?* представляет собой особую проблему, потому что в селеноцентрической системе координат эта задача двузначна (одной и той же широты можно достигнуть при сближении по направлению движения Луны и против направления движения). Для получения эффективной вычислительной схемы используются метод параметров попадания и метод перемещающейся конечной точки. Система координат для параметров попадания при встрече с Луной строится, как показано на рис. 31.6; ось Т0m находится в плоскости лунного экватора,

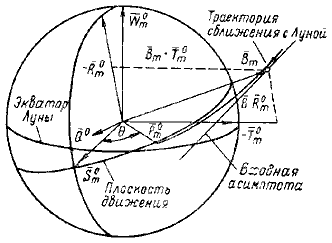
Рис. 31.6. Параметры попадания при встрече с Луной.

ось S0m параллельна входной асимптоте и расположена в плоскости движения, а ось R0m дополняет систему до правой. Параметры попадания В.Т0 и B.R 0 для заданных значений Rm и наклонения Ist

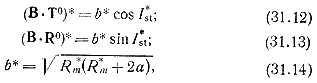
где Т 0, R0 – единичные векторы; звездочка означает требуемые конечные условия; а – большая полуось гиперболы. Как видно из рис. 31.7, траектория первого приближения достаточно точно определяет величину а. Даже когда траектория первого приближения не будет удовлетворять заданным конечным условиям, например, не достигается величина Rm*, тем не менее входная асимптота и большая полуось окажутся близкими к заданным конечным величинам. Это медленное изменение асимптоты можно классифицировать как квазипостоянство входной асимптоты гиперболической траектории. Однако параметры прицеливания содержат широту ?* вместо наклонения Ist*. Основываясь на принципе квазипостоянства входной асимптоты гиперболической траектории,

Рис. 31.7. Определение переменных для расчета параметров попадания при встрече с Луной.

можно вычислить приблизительно требуемый угол ?* между асимптотой и радиусом-вектором перицентра. Зная асимптоту, т. е. вектор Sm* после первого приближения, а также требуемые величины ?*, Rm* и ?*, можно из геометрических соотношений представить R*m и ?* через (В.Т 0)* и (B.R0)*. Для этого рассмотрим следующие уравнения (рис. 31.6):

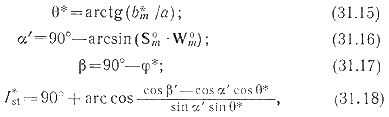
где Wm0 – единичный вектор угловой скорости вращения Луны; ?*—угол между входной асимптомой гиперболы и заданным радиусом-вектором периселения; ?'—угол между Wm0 и Sm0; ?'—угол между Wш0 и заданным радиусом-вектором периселения; Ist* – угол между Tm0 и В*m .

Так как первые вычисленные значения величин (В·Т0)* и (B-R 0)* не являются заданными, используется принцип ограничения перемещения конечной точки. Вследствие изменения входной асимптоты гиперболы изменяются также величины ?* и а. Результатом этого является медленное изменение (В·Т0)* в процессе вычислений, однако процесс быстро сходится, так что заданные величины Rm* и ?* и получаются эффективно.

Для вычисления параметров точки попадания используются формулы

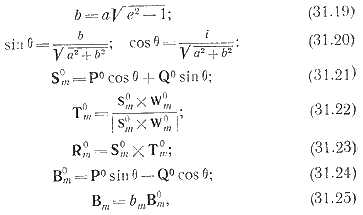
где е – эксцентриситет; b – малая полуось; ? – угол между действительным радиусом-вектором перицентра и входной асимптотой; S0m – единичный селеноцентрический вектор, параллельный входной асимптоте; Т0m – единичный вектор в плоскости лунного экватора, направленный по S0m X W0m; R0m – единичный вектор, дополняющий систему координат до правой; Р0 – единичный вектор, направленный в точку периселения;

Q0 – единичный вектор скорости в периселении; Вm вектор, направленный из центра Луны перпендикулярно входной асимптоте.

Действительные лунные параметры попадания определяются как