Евдокс Книдский, предшественник Аристотеля, создал теорию гомоцентрических сфер (дошедшую до нас лишь в пересказе Аристотеля), согласно которой каждая планета прикреплена к поверхности полой сферы, равномерно вращающейся внутри другой сферы, тоже вращающейся вокруг оси, не совпадающей с осью вращения первой сферы. В центре этих сфер находится Земля. Для представления сложного движения некоторых планет потребовалось несколько таких концентрических сфер, общее число которых доведено учеником Евдокса Калиппом до пятидесяти пяти.
Позже византийский геометр Аполлоний Пергский упростил эту теорию, заменив вращающиеся сферы кругами, и этим положил основу теории эпициклов, получившую свое завершение в сочинении Птолемея «Альмагест». Принималось, что все небесные светила движутся по окружностям и притом равномерно, а неравномерные движения планет объясняли их одновременным участием в нескольких круговых равномерных движениях, происходящих в разных плоскостях и с разными скоростями. Земля (о шарообразности и вращении которой якобы уже сообщила Пифагорейская школа) оказалась неподвижно покоящейся в центре Вселенной, что соответствовало непосредственному впечатлению от вида звездного неба.
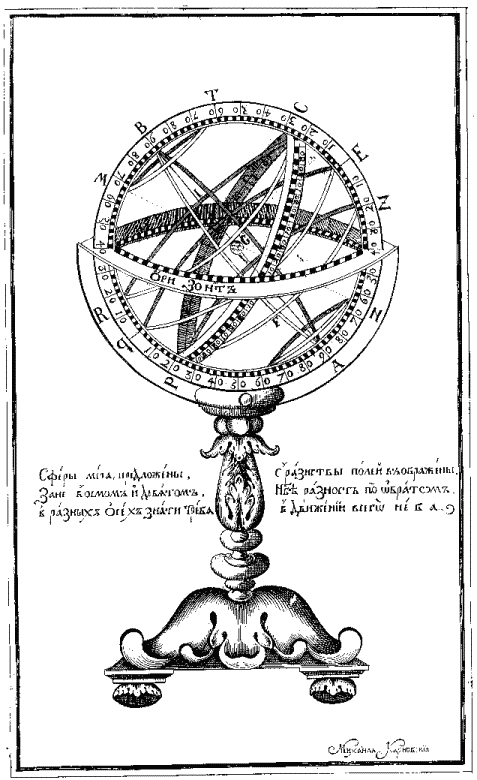
Для практического применения теория эпициклов нуждалась в значениях величин, определяющих периоды обращения планет, взаимные наклоны их орбит, длины дуг попятных движений и т. п., которые можно было получить только из наблюдений, измеряя соответствующие промежутки времени и углы. Для этого были созданы различные приспособления и инструменты, сначала простейшие, такие как гномон, а затем и более сложные – трикветрумы и армиллярные сферы.
Утверждение геоцентрической модели связано прежде всего с именем Аристотеля. Первое высказывание о бесконечности Вселенной и бесчисленности ее миров приписывают Анаксимандру.
Первую гелиоцентрическую модель планетарной системы разработал, говорят, Аристарх Самосский, предвосхитив открытие Коперника. Тем не менее гелиоцентрическая система не имела достаточных основ, то есть попросту не была нужна, а геоцентрическая до такой степени удовлетворяла всех, что Аристарх не нашел сторонников. Поэтому учение его в дальнейшем оказало так мало влияния, что даже Коперник, по-видимому, не имел о нем понятия.
Известность Аристарху доставило определение относительного расстояния Солнца от Земли и Луны, тем более что подобное астрономическое измерение было произведено им первым. Когда Луна кажется с Земли наполовину освещенной, тогда Солнце, Земля и Луна образуют прямоугольный треугольник с вершиной прямого угла на Луне. Аристарх определил угол, образуемый зрительными лучами по отношению к Луне и Солнцу, в 87° и отсюда вывел отношение одного из катетов этого треугольника к гипотенузе, то есть отношение лунного расстояния к солнечному, равным от 1:18 до 1:20. Конечно, этот результат оказался ошибочным; в действительности указанное отношение приблизительно равно 1:400.
Архимед со ссылкой на Аристарха пытался вычислить размеры мира через счет очень больших количеств. Эту идею он изложил в работе «О числе песчинок». Вот введение к этой работе:
«Есть люди, о царь Гелон, которые полагают, что число песчинок бесконечно. Другие не признают их числа бесконечным, но думают, что невозможно указать числа большего, чем их количество. Я со своей стороны постараюсь доказать геометрическим вычислением, на которое ты удостоишь обратить внимание, что между числами, находимыми в книгах Цейксиппа, есть такие, которые превосходят число песчинок, вмещаемых телом не только большим, нежели Земля, но равным по величине всей Вселенной…
Некоторые утверждают, как тебе известно, что окружность Земли приблизительно равна 300 000 стадий. Я иду гораздо дальше и принимаю окружность в 10 раз больше. Подобно большинству астрономов, я предполагаю далее, что земной поперечник больше лунного, а солнечный больше земного. Наконец, я принимаю поперечник Солнца в 30 раз больше поперечника Луны, но не свыше. Именно, Евдокс определяет поперечник Солнца в 9 раз больше лунного, Фидий – в 12 раз, а Аристарх пытается доказать, что он более чем в 18 и менее чем в 20 раз больше. Я старался при помощи инструментов измерить угол, идущий от окружности Солнца к глазу наблюдателя. Измерение это нелегко, потому что нельзя в точности определить угла посредством глаз, рук и инструментов».
При помощи своего метода, который он описывает весьма подробно, Архимед находит, что видимая величина Солнца меньше 1/655 и больше 1/800 части круга зодиака. На основании этих измерений и предыдущих допущений он приходит к выводу, что расстояние Солнца от Земли не может быть больше 10 000 земных радиусов, а поперечник сферы неподвижных звезд не больше 10 000 000 000 стадий. Число песчинок, которое наполнило бы такую Вселенную, выражается у него в конце концов числом, состоящим, по нашему счислению, из 1 с 63 нулями. Хотя Архимед полагал, что все принятые им размеры несравненно больше действительных, но на самом деле расстояние Солнца он определил на 2/5 меньше действительного, так как отношение солнечного поперечника к лунному равно не 30:1, а приблизительно 400:1. В упрек этого ему нельзя ставить. Даже у Кеплера расстояние между Солнцем и Землей меньше, чем у Архимеда.
Эратосфен – современник Архимеда. Он стал первым выдающимся географом древности и вместе с тем астрономом и филологом. Из многочисленных сочинений Эратосфена для нас наиболее интересна «География» в трех книгах, вторая из которых содержит учение о поясах, о возможности кругосветного плавания и, кроме того, отчет о знаменитом измерении земной окружности, содержащий первое в истории изложение самого способа измерения.
Существовало наблюдение, что в начале лета в Сиене, в верхнем Египте, бывает вполне освещено солнечным светом дно глубокого колодца. Солнце находилось, стало быть, в этот момент в зените над Сиеной, тогда как в Александрии оно отклонялось от зенита на 1/50 окружности круга. Эратосфен полагал, что Александрия лежит прямо на север от Сиены, и отсюда заключил, что расстояние между обоими городами равно 1/50 земного меридиана. А так как путешественники считали это расстояние равным 5 000 стадий, то Эратосфен определил земную окружность в 250 000 стадий. К сожалению, длина стадий нам в точности неизвестна.
Гиппарх, уроженец Никеи, руководил школой в Александрии. Вместе с Аристархом и Птолемеем он составил блестящую тройку византийских астрономов. Многие ставят его даже выше Птолемея, называя систему последнего лишь искусным переложением трудов Гиппарха. Для объяснения неравномерности движения планет Гиппарх выдвинул Землю на некоторое расстояние из центра планетных путей и принял последние за эксцентрические круги.
Далее, он определил расстояние Земли от центра солнечного пути (эксцентриситет) в 1/24 радиуса и определил также положение земного приближения и удаления, что дало ему возможность вычислить солнечные таблицы. При сравнении своих наблюдений летнего солнцестояния с наблюдениями Аристарха Гиппарх определил длину года в 365 дней, 5 часов и 55 минут вместо 365 1/2 дней. При помощи эксцентрического пути Луны ему удалось также объяснить главнейшую неравномерность лунного движения и по вычислению элементов этого пути составить лунные таблицы. Параллаксы Солнца и Луны (углы, под которыми виден земной радиус с этих светил) он определил в 3 и 57 и из этого вычислил относительные расстояния их от Земли в 1200 и 59 земных радиусов, – второе довольно верно; первое же в 20 раз меньше действительного.
При сравнении своих наблюдений с более древними Гиппарх нашел, что одна звезда в Деве за 150-летний период времени изменила свою долготу на 2°, и далее заметил, что такое перемещение одинаково свойственно всем неподвижным звездам и что оно объясняется движением экваториального полюса вокруг полюса эклиптики. Для установления так называемого предварения равноденствий Гиппарх должен был произвести множество определений места неподвижных звезд. В звездном каталоге Гиппарха, которым впоследствии воспользовался Птолемей, действительно указано место более 1000 неподвижных звезд.