Теперь мы можем объяснить, откуда берётся обратная квадратичная зависимость в законе Ньютона. Воображаемая сфера с центром на Солнце, проходящая через место нахождения спутника (рис. 13.4 в), имеет площадь (подобно площади поверхности любой сферы в трёхмерном пространстве), пропорциональную квадратуеё радиуса, т. е. квадратурасстояния между Солнцем и спутником. Значит, плотность линий гравитационного поля, проходящих через сферу (суммарное количество линий, поделённое на площадь поверхности сферы), уменьшается по закону обратных квадратов с увеличением расстояния между Солнцем и спутником. Если удвоить это расстояние, то одно и то же количество линий поля будет равномерно распределено по сфере, имеющей в четыре раза большую площадь, и, следовательно, гравитационное притяжение уменьшится в 4 раза на этом расстоянии. Таким образом, обратная квадратичная зависимость в законе Ньютона является отражением геометрических свойств сфер в трёхмерном пространстве.
Но если бы Вселенная имела два или даже только одно пространственное измерение, то как изменилась бы формула Ньютона? На рис. 13.5 апредставлена двумерная версия ситуации с Солнцем и вращающимся спутником. Как видно, линии гравитационного поля Солнца равномерно распределяются по окружности — аналогу сферы в двумерном пространстве. Поскольку длина окружности пропорциональна её радиусу (а не квадрату радиуса), то при удвоении расстояния между Солнцем и спутником плотность линий поля уменьшается в 2 раза (а не в 4 раза), из-за чего сила гравитационного притяжения падает только в 2 раза (а не в 4). Если Вселенная имела бы только два пространственных измерения, то гравитационная сила была бы обратно пропорциональна расстоянию, а не квадрату расстояния.
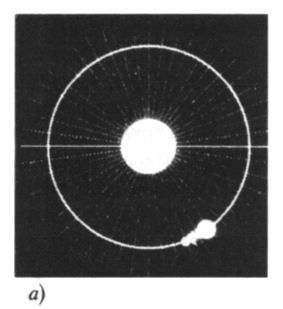

Рис. 13.5.( а) Во Вселенной только с двумя пространственными измерениями гравитационная сила падает пропорционально расстоянию, поскольку линии гравитационного поля однородно распределяются по окружности, длина которой пропорциональна её радиусу. ( б) В одномерной Вселенной у линий гравитационного поля совсем не было бы места для пространственного расхождения, так что гравитационная сила была бы постоянной, независимо от расстояния
Если Вселенная имела бы лишь одно пространственное измерение, как на рис. 13.5 б, то закон всемирного тяготения был бы ещё проще. У линий гравитационного поля вообще бы не было места для пространственного расхождения, так что сила гравитации не уменьшалась бы с расстоянием. Если удвоить расстояние между Солнцем и спутником (при условии, что подобные объекты могли бы существовать в такой Вселенной), то спутник будет пронизывать всегда одно и то же количество линий поля и, следовательно, сила гравитации между Солнцем и спутником вообще не изменялась бы.
Ситуация, проиллюстрированая на рис. 13.4 и 13.5, напрямую распространяется на Вселенную с четырьмя, пятью, шестью и более пространственными измерениями, хотя это уже невозможно изобразить. Чем больше пространственных измерений, тем больше места для расхождения линий гравитационного поля. А чем больше места, тем всё более ощутимее падает сила гравитации с увеличением расстояния между объектами. Во Вселенной с четырьмя пространственными измерениями сила гравитации падала бы обратно пропорционально третьей степени расстояния (при удвоении расстояния сила уменьшалась бы в 8 раз); в пяти пространственных измерениях эта сила падала бы обратно пропорционально четвёртой степени расстояния (при удвоении расстояния сила уменьшалась бы в 16 раз); в шести пространственных измерениях эта сила падала бы обратно пропорционально пятой степени расстояния (при удвоении расстояния сила уменьшалась бы в 32 раза); и так далее с увеличением количества пространственных измерений Вселенной.
Вы могли бы подумать, что успешное объяснение громадного объёма данных с помощью закона обратных квадратов (от движения планет до траекторий комет) подтверждает то, что мы живём во Вселенной с тремя пространственными измерениями. Но такой вывод был бы поспешным. Нам известно, что закон обратных квадратов работает на астрономических масштабах, {177} и мы знаем, что он работает на земных масштабах, и это согласуется с тем фактом, что на таких масштабах мы видим три пространственных измерения. Но известно ли нам, что он работает и на более мелких масштабах? Насколько он был проверен в микрокосмосе? Оказывается, эксперименты подтвердили его лишь до десятой доли миллиметра; если два объекта разделяет расстояние, превышающее десятую часть миллиметра, то сила их гравитационного притяжения точно соответствует обратной квадратичной зависимости. Но пока что экспериментаторы наталкиваются на значительные технические трудности при проверке закона всемирного тяготения на более мелких масштабах (это связано со слабостью гравитационного взаимодействия и квантовыми эффектами). Этот вопрос очень важен, поскольку отклонение от закона обратных квадратов явилось бы убедительным сигналом, указывающим на существование дополнительных измерений.
Чтобы наглядно представить это, давайте рассмотрим модельную задачу с меньшим количеством пространственных измерений, что позволит нам легко обрисовать и проанализировать всю картину. Вообразим, что мы живём в одномерной Вселенной, — точнее, мы так думаем, поскольку мы видим только одно пространственное измерение и, кроме того, столетия экспериментальных проверок показали, что сила гравитации не меняется с изменением расстояния между объектами. Также представим, что за все эти столетия закон гравитации был проверен на расстояниях вплоть до десятой доли миллиметра, но не ближе. Для меньших расстояний просто нет экспериментальных данных. Вообразим далее, что на самом деле Вселенная имеет второе, свёрнутое пространственное измерение, так что её форма похожа на туго натянутый канат Филиппа Пети, как представлено на рис. 12.5. Как это скажется на будущих более точных проверках закона гравитационного притяжения? Ответ можно получить, глядя на рис. 13.6. Как только два крохотных объекта окажутся достаточно близко друг к другу (на расстоянии порядка длины окружности свёрнутого измерения), двумерный характер пространства станет непосредственно очевиден, поскольку на этих масштабах у линий гравитационного поля будетместо для расхождения (рис. 13.6 а). На достаточно близком расстоянии сила гравитации окажется обратнопропорциональной расстоянию между объектами, перестав быть постоянной и не зависящей от расстояния.


Рис. 13.6.( а) Когда объекты близки, сила гравитации меняется как в двумерном пространстве. ( б) На больших расстояниях гравитационное притяжение ведёт себя как в одномерном пространстве — оно постоянно
Таким образом, если бы вы были экспериментатором в этой Вселенной и разработали бы достаточно точные методы измерения гравитационного притяжения, то вот что бы вы обнаружили. Когда два объекта находятся очень близко друг к другу, на расстоянии, гораздо меньшем, чем размер свёрнутого измерения, то их гравитационное притяжение уменьшалось бы пропорционально расстоянию между ними. Но когда расстояние между объектами становится бо?льшим, чем длина окружности свёрнутого измерения, то всё бы изменилось. Теперь линиям гравитационного поля просто некуда расходиться. Они бы максимально заполнили второе свёрнутое измерение (можно сказать, они бы «насытили» его), так что начиная с этого расстояния гравитационная сила больше бы не уменьшалась, как проиллюстрировано на рис. 13.6 б. Можно сравнить это насыщение с водопроводной системой в старом доме. Представьте, что вы принимаете душ в ванной комнате этого дома и только что намылили себе голову. И, вот досада, кто-то открывает кран на кухне, и напор воды падает, потому что вода теперь распределяется по двум кранам. Напор уменьшится ещё больше, если кто-то откроет кран в постирочной комнате, поскольку вода побежит и туда. Но как только все водопроводные краны в доме открыты, напор воды перестаёт падать. Хотя струя воды в душе уже не такая сильная, как вам хотелось бы, но теперь вам нечего бояться — напор воды останется постоянным, так как вода полностью распределилась по всем «дополнительным» кранам. Аналогично, как только гравитационное поле полностью распространилось по дополнительному свёрнутому измерению, сила притяжения перестаёт уменьшаться с увеличением расстояния.