64

Вы можете поинтересоваться, как обсуждение в этой главе соотносится с нашим описанием в главе 3 объектов, «всегда двигающихся» через пространство-время со скоростью света. Для не склонного к математике читателя грубый ответ состоит в том, что история объекта представляется кривой в пространстве-времени — путём через блок пространства-времени, который высвечивает каждое место, которое занимал объект в момент, когда он там был (примерно так, как мы видим на рис. 5.1). Интуитивное обозначение «движения» через пространство-время тогда может быть выражено на языке «без течения», путём просто указания этого пути (в противоположность представлению, что путь проходится на ваших глазах). «Скорость», связанная с этим путём, тогда измеряется величиной, определяемой длиной этого пути (от одной выбранной точки до другой), делённой на промежуток времени, измеренный часами, переносимыми кем-то или чем-то между двумя выбранными точками пути. Ещё раз, это есть подход, который не содержит какого-либо течения времени: вы просто смотрите на то, что говорят интересующие вас часы в двух представляющих интерес точках. Оказывается, что скорость, найденная таким способом, для любогодвижения равна скорости света. Математически подготовленный читатель немедленно обнаружит причину этого. Метрика в пространстве-времени Минковского есть

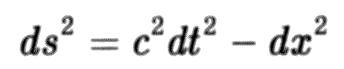
(где dx ²есть евклидова длина

), тогда как время, измеряемое движущимся часами («собственное» время), даётся выражением dt ²= ds ²/ c ². Так что, очевидно, скорость движения через пространство-время, определяемая выражением ds/ dt, равна c.

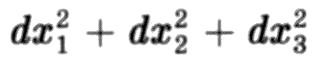
65

Carnap S. R. Autobiography, in The Philosophy of Rudolf Carnap.P. A. Schilpp, ed. Chicago: Library of Living Philosophers, 1963. P. 37.

66

Отметим, что асимметрия, о которой идёт речь (стрела времени), возникает из порядка, в котором события имеют место вовремени. Вы могли бы также поинтересоваться асимметрией самого времени — например, как мы увидим в дальнейших главах, в соответствии с некоторыми космологическими теориями время могло иметь начало, но оно может не иметь конца. Это разные понятия асимметрии времени, но наше обсуждение здесь сосредоточено на первом. Но даже в этом случае до конца главы мы придём к заключению, что асимметрия вещей во времени имеет отношение к специальным условиям в ранней истории Вселенной, а потому связывает стрелу времени с космологией.

67

Для склонного к математике читателя позвольте мне отметить более точно, что означает симметрия по отношению к обращению времени, и указать на одно интригующее исключение, значение которого для обсуждаемых нами в этой главе проблем ещё предстоит полностью осознать. Простейшее определение симметрии по отношению к обращению времени состоит в утверждении, что набор законов физики симметричен по отношению к обращению времени. Если задано любое решение уравнений, скажем S( t), тогда S(? t) тоже будет решением этих уравнений. Например, в ньютоновской механике с силами, которые зависят от положений частиц, если x( t) = ( x ₁( t), x ₂( t), ..., x _{3 n}( t)) есть положения nчастиц в трёх пространственных измерениях, то из того, что x( t) является решением уравнений d ² x( t)/ dt ²= F( x( t)), следует, что x(? t) также является решением уравнений Ньютона d ² x(? t)/ dt ²= F( x(? t)) Отметим, что x(? t) представляет движение частиц, которые проходят через те же самые положения, что и в случае x( t), но в обратном порядке и с противоположными скоростями.

В более общем смысле набор физических законов обеспечивает нас алгоритмом эволюции из начального состояния физической системы в момент времени t ₀к состоянию в некоторый другой момент времени t+ t ₀. Конкретно, этот алгоритм может быть рассмотрен как отображение U( t), которое действует на начальное состояние S( t ₀) и приводит к состоянию S( t+ t ₀), т. е. S( t+ t ₀) = U( t) S( t ₀). Мы говорим, что законы, приводящие к U( t), являются симметричными во времени, если имеется отображение T, удовлетворяющее соотношению U(? t) = T ^?1 U( t) T. На обычном языке это уравнение говорит, что при помощи подходящих манипуляций над состоянием физической системы в один момент времени (достигаемых с помощью T) эволюция на время tвперёд во времени в соответствии с законами теории (выражаемыми через U( t)) становится эквивалентной эволюции системы на tединиц времени назад (обозначаемой U(? t)). Например, если мы определи состояние системы частиц в один момент времени через их положения и скорости, тогда Tбудет оставлять все положения частиц фиксированными и менять на противоположные все скорости. Эволюция такой конфигурации частиц вперёд во времени на промежуток tэквивалентна эволюции оригинальной конфигурации частиц назад во времени на промежуток t. (Действие T ^?1отменяет обращение скоростей так, что в конце не только положения частиц совпадают с теми, которые они имели tединиц времени назад, но то же будет и с их скоростями.)

Для некоторых законов оператор Tболее сложен, чем в случае ньютоновской механики. Например, если мы изучаем движение заряженных частиц в присутствии электромагнитного поля, одно только обращение скоростей частиц не приведёт к движению, в котором частицы проходят те же шаги в обратном порядке. Должно быть обращено также и направление магнитного поля. (Это требуется, чтобы член ?? Bв уравнении для силы Лоренца остался неизменным.) Таким образом, в этом случае операция Tвыполняет оба эти преобразования. Тот факт, что мы проделываем больше, чем просто обращаем все скорости частиц, никак не влияет на обсуждение, которое следует дальше в тексте. Всё, что имеет значение, это то, что движение частицы в одном направлении точно так же согласуется с законами физики, как и движение частицы в обратном направлении. То, что мы обращаем любые магнитные поля, которым случилось присутствовать, чтобы полностью обратить движение частиц, не имеет особого значения.

Ситуация становится более тонкой в случае слабых ядерных взаимодействий. Слабые взаимодействия описываются частным случаем квантовой теории поля (которая коротко обсуждается в главе 9), и общая теорема показывает, что квантовые теории поля (при условии, что они локальны, унитарны и Лоренц-инвариантны, — такие и представляют интерес) всегда симметричны относительно объединенияопераций сопряжения заряда C(которые заменяют частицы на их античастицы), чётности P(которые отражают координаты относительно начала) и чистой операции обращения времени T(которая заменяет tна ? t). Так что мы можем определить оператор Tкак CPT, но если T-инвариантность безусловно требует введения операции CP, тогда Tбольше не может быть интерпретирован просто как прохождение частицами их движения в обратном направлении (поскольку, например, сам тип частицы будет изменён таким T— частицы будут заменены их античастицами, — а потому обратного движения оригинальных частиц уже не может быть). Оказалось, что имеются некоторые экзотические экспериментальные ситуации, в которых реализуется именно этот случай. Есть определённые виды частиц (K-мезоны, B-мезоны), манера поведения которых CPT-инвариантна, но не инвариантна относительно чистой операции обращения времени T. Это было установлено косвенно в 1964 г. Джеймсом Кронином, Валом Фитчем и их сотрудниками (за что Кронин и Фитч получили в 1980 г. Нобелевскую премию), которые показали, что K-мезоны нарушают CP-симметрию (следовательно, они должны нарушать T-симметрию, чтобы не нарушать CPT-симметрию). Позднее нарушение T-симметрии было непосредственно установлено в эксперименте CPLEARв ЦЕРНе и в эксперименте KTEVв Фермилабе. Грубо говоря, эти эксперименты продемонстрировали, что если вам показали фильм с записью процессов, происходящих с этими мезонами, то вы будете в состоянии определить, прокручивается ли этот фильм в правильном направлении, или в обратном. Другими словами, эти особые частицы могут различать прошлое и будущее. Остаётся неясным, однако, имеет ли это какое-нибудь отношение к стреле времени, которую мы ощущаем в повседневном контексте. Как-никак, это экзотические частицы, которые могут быть рождены на короткие моменты в высокоэнергетических столкновениях, но они не являются частями привычных материальных объектов. Для многих физиков, включая меня, кажется маловероятным, что необратимость времени, проявляемая этими частицами, играет роль в разрешении загадки стрелы времени, так что мы не будем дальше обсуждать этот исключительный пример. Но правда заключается в том, что никто не знает этого с уверенностью.