Животрепещущий вопрос таков: почему мы никогда этого не видим? Я думаю, можно смело заключать пари, что никто никогда на самом деле не был свидетелем восстановления разбитого яйца.
Но если законы физики допускают это, и более того, если эти законы рассматривают разбивание и восстановление яйца одинаково, то почему одно никогда не происходит, в то время как другое имеет место?
Симметрия по отношению к обращению времени
В качестве первого шага к решению этой головоломки нам надо понять в более конкретных терминах, что означает для известных законов физики быть симметричными по отношению к обращению времени. С этой целью представьте, что идёт XXV в. и вы играете в теннис в новой межпланетной лиге с вашим партнёром по имени Вильямс «Мощный удар». Немного не привыкший к уменьшенной гравитации Венеры, «Мощный удар» делает сильнейший удар слева и запускает мяч в глубокую темноту пространства. Пересекающий пространство космический шаттл производит киносъёмку мяча, когда тот пролетает рядом, и посылает ленту в CNN (Celestial News Network — небесная сеть новостей) для телевещания. Возникает вопрос: если техники CNN сделали ошибку и запустили плёнку о теннисном мяче в обратном направлении, есть ли какой-нибудь способ это определить? Если вы знали направление и ориентацию камеры во время съёмок, то вы будете в состоянии распознать их ошибку. Но смогли бы вы распознать ошибку, просмотрев только саму плёнку без дополнительной информации? Ответ: нет. Если в правильном направлении времени (вперёд) плёнка показывает мяч летящим слева направо, то в обратном направлении он будет показан летящим справа налево. И, конечно, законы классической физики позволяют теннисным мячам двигаться как налево, так и направо. Так что движение, которое вы видите, когда плёнка прокручивается как в прямом, так и в обратном направлении, превосходно согласуется с законами физики.
Пока мы считали, что на теннисный мяч не действуют никакие силы, поэтому он двигается с постоянной скоростью. Рассмотрим теперь более общую ситуацию, включив силы. Согласно Ньютону, влияние силы заключается в изменении скорости объекта: силы сообщают ускорения. Представим, что после некоторого времени плавания в пространстве мяч попадает под влияние гравитационного притяжения Юпитера, что заставляет его двигаться с возрастающей скоростью по нисходящей дуге, развёрнутой направо к поверхности Юпитера, как показано на рис. 6.1 аи б. Если вы проигрываете плёнку с этим движением в обратном направлении, теннисный мяч будет двигаться по дуге, которая развёрнута вверх и налево от Юпитера, как на рис. 6.1 в.
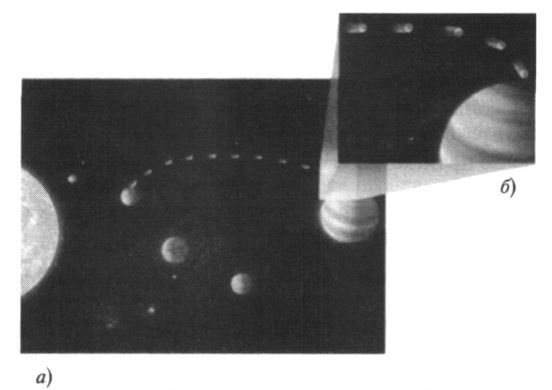
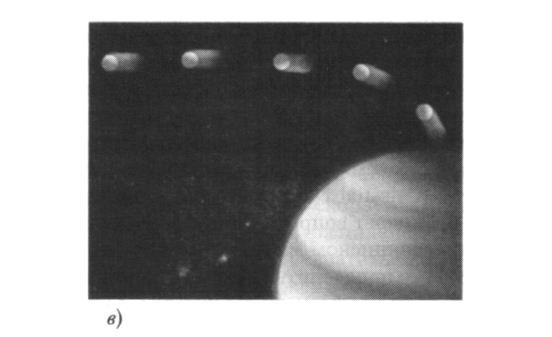
Рис. 6.1.( а) Теннисный мяч, летящий от Венеры к Юпитеру. ( б) Окончание полёта. ( в) Движение теннисного мяча, если его скорость изменена на противоположную прямо перед столкновением с Юпитером
Возникает новый вопрос: является ли движение, демонстрируемое на плёнке, которая проигрывается в обратном направлении, — движение, обратное во времени по отношению к движению, в действительности снятому на плёнку, — допустимым по классическим законам физики? Может ли такое движение произойти в реальном мире? На первый взгляд, ответ «да»кажется очевидным: теннисные мячи могут двигаться по нисходящим дугам направо, или по восходящим дугам налево, или по бесконечному количеству других траекторий. Тогда в чём трудность? Хотя ответ, несомненно, «да», наши рассуждения поверхностны и упускают реальную суть вопроса.
Когда вы начинаете прокручивать плёнку в обратном направлении, вы видите, как теннисный мяч отскакивает от поверхности Юпитера и начинает двигаться вверх и налево в точности с той же скоростью (но в точности в противоположном направлении), с которой он падал на планету.
Начальная часть плёнки определённо согласуется с законами физики: например, мы можем представить, что кто-то запустил теннисный мяч с поверхности Юпитера с точно такой же скоростью. Существенный вопрос состоит в том, будет ли и оставшаясячасть обратного движения также согласовываться с законами физики. Будет ли мяч, запущенный с этой начальной скоростью и подвергающийся воздействию притягивающей вниз гравитации Юпитера, действительно двигаться вдоль траектории, изображённой на оставшейся части прокручиваемой в обратном направлении плёнки? Будет ли он в точности очерчивать его оригинальную нисходящую траекторию, но в обратном направлении?
Ответ на этот уточнённый вопрос — да. Во избежание путаницы, разберёмся более детально. На рис. 6.1 а, перед тем, как гравитация Юпитера оказала существенное влияние, мяч двигался точно вправо. Далее, на рис. 6.1 бмощная гравитационная сила захватила мяч и притянула его к центру планеты — притяжение, которое в большей степени направлено вниз, но, как вы можете видеть на рисунке, частично вправо. Это означает, что когда мяч приблизился к поверхности Юпитера, его ориентированная вправо скорость немного увеличилась, а компонента скорости, направленная вниз, значительно увеличилась. Следовательно, в прокручиваемой назад плёнке взлёт мяча с поверхности Юпитера будет происходить в направлении немного влевои преимущественно вверх, как показано на рис. 6.1 в.
При этой стартовой скорости гравитация Юпитера будет оказывать максимальное влияние на скорость мяча, направленную вверх, делая её всё меньше и меньше, тогда как скорость мяча, направленная влево, тоже будет уменьшаться, но в меньшей степени. И с быстро уменьшающейся компонентой скорости, направленной вверх, движение мяча будет становиться преимущественно таким, при котором преобладает скорость, направленная влево, что вынудит мяч следовать влево по выгнутой вверх траектории. Вблизи окончания этой дуги гравитация истощит всё направленное вверх движение, также как и добавочную скорость, направленную вправо, которую гравитация Юпитера добавила мячу во время его пути вниз, оставив движение мяча в направлении влево в точности с той же скоростью, которую он имел при его первоначальном приближении к Юпитеру.
Всё это можно просчитать, но суть в том, что эта траектория в точности совпадает с обратным начальным движением мяча. Просто изменив скорость мяча на противоположную, как на рис. 6.1 в, — отправив его в путь с той же скоростью, но в противоположном направлении, — его можно заставить пройти полностью свою исходную траекторию, но в обратном направлении. Возвращаясь к плёнке, мы видим, что выгнутая вверх траектория, направленная влево, — траектория, которую мы просто сконструировали, основываясь на ньютоновских законах движения, — в точности совпадает с той, что мы видели при прокручивании плёнки назад. Так что движение мяча с обращением времени, как изображено на прокручиваемой назад плёнке, согласуется с законами физики так же хорошо, как и его движение в прямом времени. Движение, которое мы видели, прокручивая плёнку в обратном направлении, есть движение, которое на самом деле может происходить в реальном мире.
Хотя имеется несколько тонкостей, которые я переношу в примечания, этот вывод является общим. {67} Все известные и признанные законы, относящиеся к движению, — от уже обсуждавшейся выше ньютоновской механики до электромагнитной теории Максвелла и специальной и общей теории относительности Эйнштейна (вспомним, что мы исключили из рассмотрения квантовую механику до следующей главы) — заключают в себе симметрию по отношению к обращению времени: движение, которое может происходить в обычном направлении, соответствующем прямому ходу во времени, может так же происходить и в обратном направлении. Поскольку терминология несколько запутанная, позвольте ещё раз подчеркнуть, что мы не изменяем направление самого времени. Время действует так же, как и всегда. Наши выводы таковы, что мы можем заставить объект пройти его траекторию в обратном направлении путём простой процедуры обращения его скорости в любой точке на его пути. Иными словами, обращение скорости объекта в некоторой точке его пути заставит объект совершить движение, которое мы видели на прокручиваемой назад плёнке.