Смысл математической обработки заключается в следующем. Надо убедиться в том, что полученные различия не случайны. Дело в том, что результаты отдельных экспериментов, даже сделанных в абсолютно одинаковых условиях, могут немного различаться между собой. Это связано с погрешностью измерений и чисто случайными факторами, которые всегда присутствуют в природе. Посмотрим на данные, полученные в контрольной группе. Мы видим, что количество микробов в различных экспериментах неодинаково: оно колеблется от 24 до 32 млн, хотя условия во всех пяти сосудах ничем не различались. Нам надо выяснить, не случайны ли различия как между контрольной и экспериментальными группами, так и между разными экспериментальными группами. Для этого существуют методы математической статистики. Эта наука представляет собой раздел математики, изучающий закономерности в количественных результатах наблюдений и экспериментов. В частности, с её помощью можно решить вопрос о том, насколько велика вероятность того, что полученные различия вызваны чисто случайными причинами. Если она окажется малой, то можно будет считать, что наше воздействие действительно влияет на изучаемое явление. В таком случае говорят, что это влияние является достоверным. В противном случае оно считается недостоверным и не может приниматься в расчёт в научном исследовании. Часто, для того чтобы убедиться в достоверности полученных результатов, приходится ставить очень много экспериментов, так как математическая статистика работает тем точнее, чем с большим количеством материала она имеет дело.
Итак, полученные в исследовании данные можно представить в виде таблиц. Однако использование специальных рисунков – диаграмм значительно облегчает восприятие результатов исследования. Диаграммы наглядно изображают зависимость между различными величинами. Одним из видов диаграмм являются диаграммы-линии, или графики. Построим график, иллюстрирующий данные нашего эксперимента (рис. 28, А).
Нам надо представить зависимость между концентрацией изучаемого вещества и количеством бактерий в 1 мм3 питательного раствора. Эти величины называются переменными. Концентрацию вещества мы считаем независимой переменной, так как можем задавать и изменять её по собственному усмотрению. Количество же бактерий считается зависимой переменной, поскольку она непосредственно зависит от первой величины и у нас нет других возможностей на неё повлиять. В математике эти величины называются соответственно аргументом и функцией. Таким образом, на графике будет изображена функциональная зависимость количества бактерий от количества введённого в среду препарата.
На оси абсцисс отложим значения количества введённого препарата, а на оси ординат – среднее по всем опытам количество бактерий, обнаруженное во взятой пробе. От каждой точки на обеих осях проведём перпендикулярные прямые. Точка их пересечения и будет показывать, какое количество бактерий соответствует данному количеству добавленного препарата.
В результате мы получили четыре точки, соответствующие 0; 1; 5 и 10 мг препарата. Далее мы можем рассуждать так. В эксперименте мы не использовали промежуточные количества вещества, например 0,7; или 8 мг.
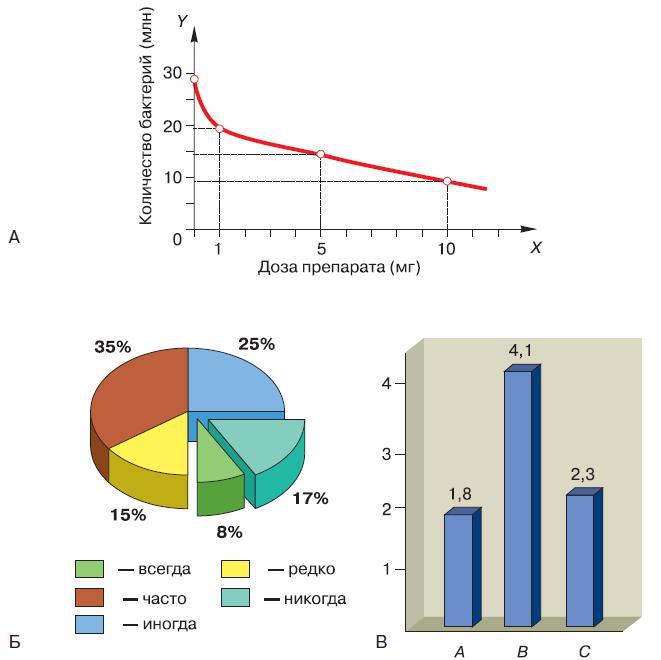
Рис. 28. Примеры непрерывного графика (А), круговой (Б) и столбчатой (В) диаграммы
А какое количество бактерий мы бы обнаружили в этих случаях? Логично предположить, что это значение, например, для 7 мг находилось бы где-то между 14,8 млн и 9 млн. Мы имеем право считать, что между концентрацией вещества и количеством микроорганизмов существует непрерывная зависимость. Эта зависимость изображается на графике плавной кривой, соединяющей проставленные точки.
Часто на графиках в качестве независимой переменной выступает время. В этом случае график показывает, как изменяется какой-то показатель с течением времени, т. е. динамику развития этого показателя. Предположим, что мы определяли количество бактерий в нашем опыте не только через два часа после начала эксперимента, но также в самом его начале, через час и через три часа, и получили следующие данные (в среднем по всем экспериментам) (табл. 3).
Таблица 3
Динамика изменений количества бактерий
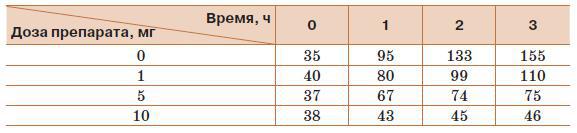
В этом случае мы можем построить график, где по оси ординат будет отложено время, прошедшее после добавления препарата, а по оси абсцисс – количество бактерий, обнаруженное в данное время при данной дозе вещества. Полученные точки надо соединить четырьмя кривыми, каждая из которых покажет динамику размножения бактерий при определённой концентрации препарата.
Однако не во всех случаях можно соединять точки плавными линиями, так как зависимость между переменными не всегда представляет собой непрерывную функцию. Например, если мы оценивали популярность телепрограмм и оказалось, что программа А в среднем была оценена на 1,8 балла, программа Б – на 4,1 балла, а программа В – на 2,3 балла, то плавной линии проводить нельзя, так как каждая программа существует сама по себе и переходов между ними нет. В этом случае используют столбчатую диаграмму, или гистограмму (рис. 28, Б). Существуют и другие виды диаграмм: круговые, сетчатые, диаграммы-области и пр. (рис. 28, В). Исследователь должен в каждом случае определять, какой вид диаграммы ему лучше использовать для демонстрации своих результатов.
1. Что означает выражение «полученные данные недостоверны»?
2. Что называется зависимой и независимой переменными? Какая из этих переменных обычно откладывается по оси абсцисс, а какая – по оси ординат?
3. В каком случае данные на графиках изображаются плавными кривыми, а в каких – столбчатыми диаграммами?
4. С помощью какого вида диаграмм удобнее всего отразить состав атмосферного воздуха; динамику изменения численности хищников и жертв в природном сообществе; процентное соотношение людей разных возрастных групп, живущих в городе?
1. Начертите матрицу. Пусть её строки означают школьные предметы, а столбцы – месяцы или четверти учебного года. В пересечения строк и столбцов занесите полученные оценки. Что означают средние величины, вычисленные по столбцам, а что – средние величины, вычисленные по строкам? Постройте графики, отражающие динамику вашей успеваемости.
2. Разработайте анкету социального опроса об отношении к природе. Проведите опрос. Проанализируйте полученные данные и представьте их в виде информационного блока на сайте школы или в стенгазете.
§ 9 Математическое моделирование
Если мы действительно что-то знаем, то мы знаем это благодаря изучению математики.
В процессе изучения окружающего мира и создания всевозможных механизмов и приспособлений человек всегда использовал метод моделирования. Суть этого метода заключается в том, чтобы заменить изучаемый или конструируемый объект его подобием, более или менее соответствующим оригиналу. Сначала понятие модели относили только к материальным объектам, например манекен мог служить моделью человеческого тела. Существовали также уменьшенные модели для самолётов, плотин и т. п. В дальнейшем понятие «модель» получило более широкое толкование. В настоящее время моделью называют некий материальный предмет или абстрактное понятие, которые содержат главные особенности изучаемого объекта или явления. В частности, любая научная гипотеза или теория является моделью протекающих в природе процессов. Особенное значение приобретают математические модели