1. Подберите эпиграф к данному параграфу.

2. Приведите пример какой-либо природной или искусственной системы. Опишите входящие в неё элементы, их взаимодействие и свойства этой системы как целого.

Методы исследования систем зависят от величины систем, их сложности и степени точности установления связей между элементами системы. В простейшем случае, если система состоит из небольшого числа элементов, между каждой их парой могут быть установлены связи. Если такая связь существует, то это значит, что между элементами существуют какие-то отношения. Представим себе систему из трёх девушек, которых зовут Даша, Маша и Катя. При этом Даша знакома и с Машей, и с Катей, а Маша и Катя между собой не знакомы. Изобразим эту систему (рис. 193).

То, что представлено на рисунке, называют графом. Граф – это фигура, состоящая из точек и линий, соединяющих некоторые точки.

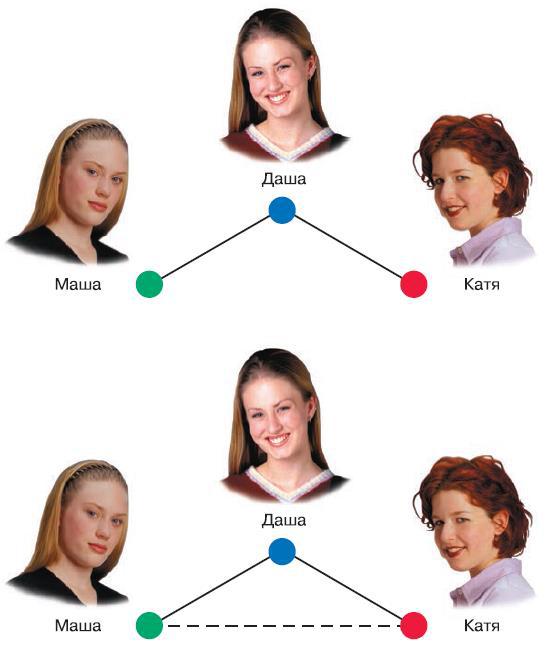
Рис. 193. Граф, иллюстрирующий взаимоотношения между Машей, Катей и Дашей

Точки называют вершинами графа, а линии – рёбрами. Если между всеми элементами системы установлены связи, то каждая вершина соединена рёбрами с любой другой. Такой граф называют полным. В нашей группе из трёх девушек полный граф получится, если Маша познакомится с Катей. Если же, напротив, Даша куда-нибудь уедет и перестанет общаться как с Машей, так и с Катей, то в графе не останется ни одного ребра, и он станет пустым.

Пока мы установили только наличие отношений между девушками, но не выяснили, какие это отношения. Предположим, что все три девушки знакомы между собой, но Даша дружит и с Машей, и с Катей, однако при этом Маша Катю недолюбливает. Чтобы изобразить эти отношения в виде графа, надо сделать так, чтобы рёбра имели положительный или отрицательный смысл. Для этого можно поставить над ними знак «+» или «-» или, как это часто делается, положительную связь изобразить в виде сплошной линии, а отрицательную – в виде пунктира.

Таким способом мы определили характер отношений между членами группы, однако в некоторых случаях этого бывает недостаточно. Иногда требуется выяснить не только наличие и знак связи, но и направление, в котором один элемент системы влияет на другой. Можно найти много примеров, когда один из элементов влияет на состояние другого, но тот не оказывает никакого действия на первый. Учитель может научить школьника химии, но ученик вряд ли что-нибудь добавит к знаниям учителя по этому предмету. Погода влияет на урожай свёклы, но урожай свёклы никак не влияет на погоду. В этом случае мы изобразим рёбра графа не просто чёрточками, а стрелками, показывающими, в каком направлении оказывается влияние. Такой граф называют организованным графом или сокращенно орграфом. В этом случае влияние также может быть положительным или отрицательным, что обозначается знаками около стрелок или типом линии, с помощью которой они изображаются.

Во многих случаях элементы в каждой паре оказывают взаимное влияние друг на друга. Такое отношение называют обратной связью и изображают на графе двумя противоположно направленными стрелками. В зависимости от характера воздействия, т. е. от знаков, которые приписываются этим стрелкам, можно выделить три типа обратных связей.

Отрицательная обратная связь, или плюс-минус взаимодействие, обеспечивает стабильность системы, невозможность выхода её состояния за определённые пределы. Мы уже рассматривали пример отрицательной обратной связи в § 9, где говорили об экологических моделях. Представьте себе систему из двух элементов A и B, которые связаны таким образом, что A усиливает B, а B ослабляет A. Что будет, если состояние одного из элементов немного изменится? Допустим, что величина A увеличилась. За этим тотчас же последует увеличение B. Но это увеличение вызовет снижение A, и в результате система останется в прежнем состоянии или, как в случае лис и зайцев, будет совершать колебания около некоего среднего значения. Поэтому такой тип взаимодействия называют также стабилизирующей обратной связью. Отрицательная обратная связь часто встречается в природных биологических процессах и широко применяется в разнообразных технических приспособлениях. Простым известным примером может быть устройство сливного бачка, где поступающая вода поднимает поплавок, который прекращает дальнейшее поступление воды.

Отрицательная обратная связь имеет огромное значение для устойчивости природных и технических систем. Но легко понять, что, если бы все системы были абсолютно устойчивы, было бы невозможно никакое развитие. Изменения в системах обеспечиваются ещё двумя типами обратных связей. Одну из них называют положительной обратной связью. Она состоит в том, что оба элемента в паре усиливают друг друга. Если вывести такую систему из равновесия, немного усилив элемент A, то элемент B тоже усилится, что приведёт к дальнейшему увеличению A и т. д. В результате оба элемента будут постоянно возрастать до возможного в этих условиях предела. Такая ситуация часто возникает в группе людей и приводит к разрастанию возникшего скандала или паники. Если же нарушение равновесия выразится в уменьшении A, то это приведёт к уменьшению B, и процесс будет продолжаться до тех пор, пока оба элемента не достигнут своих минимальных значений. Такую картину можно наблюдать в экологических системах, где между двумя видами живых организмов существуют симбиотические отношения, т. е. отношения взаимопомощи (рис. 194).

Третий тип обратной связи называют антагонистической связью, она выражается в подавлении каждым элементом своего партнёра. Если один из элементов случайно усилится, то это приведёт к ослаблению второго элемента и вслед за этим – к дальнейшему усилению первого. Процесс будет продолжаться до тех пор, пока один элемент не достигнет максимального, а второй – минимального значения. Примером может служить экологическая ситуация, когда два вида находятся в конкурентных отношениях.

Существует, однако, множество систем, в которых мы не можем установить точных связей между элементами потому, что эти связи очень сложны, или потому, что элементов очень много и за ними невозможно пронаблюдать. Для изучения таких систем используют другие методы исследования.

Рис. 194. Опыление цветков пчёлами – пример симбиотических взаимоотношений

На заре кибернетики появилось и широко использовалось понятие чёрного ящика, под которым понималась система, слишком сложная для непосредственного изучения, но для которой можно установить связь между её входами и выходами. Для этого надо наблюдать, что воздействует на систему, или искусственно воздействовать на неё, одновременно следя за ответной реакцией, т. е. зная, что есть «на входе», следить за результатами «на выходе» системы[23].

В некоторых случаях можно установить однозначную связь между состоянием входов (воздействия) и состоянием выходов (реакции) при том, что мы не можем в точности знать, как ведёт себя каждый из элементов системы. Но ведь мы убеждены в том, что результат определяется именно этими элементами. Как же нам описать их поведение? Не имея возможности точно определить характеристики этих элементов, мы можем оценить их приблизительно, с какой-то степенью допуска. Здесь мы опять сталкиваемся с проблемой отношения детерминизма и случайности. Если мы не можем установить, как ведёт себя в точности молекула в сосуде с газом, муравей в муравейнике или человек в государстве, мы должны считать это поведение в большей или меньшей степени случайным. Но что означает «в большей или меньшей»? Как измерить случайность? Для этого существует понятие математической вероятности, с которым мы познакомимся в следующем параграфе.