Динамические методы определения П. С. основаны на изучении возмущений в движении планет и Луны, вызываемых притяжением других небесных тел. П. С. p

и суммарная масса Земли и Луны М , выраженная в единицах массы Солнца, связаны соотношением

  p

,

вытекающим из 3-го закона Кеплера. П. С. вычисляется, если определена общая масса Земли и Луны, по возмущениям, вызываемым этими телами в движении какой либо планеты. Существуют и другие динамические методы определения П. С.

  Физические методы определения П. С., в частности, основаны на соотношении между средней скоростью V движения Земли по гелиоцентрической орбите (около 29,8 км/сек ) и большой полуосью а этой орбиты, т. е. в конечном счёте с П. С. Скорость V можно определить: измеряя лучевые скорости звёзд, лежащих вблизи эклиптики; определяя постоянную годичной аберрации c (см. Аберрация света ), равную отношению V к скорости света; измеряя доплеровские смещения радиолиний (с длиной волны 21 см ) в спектрах межзвёздных водородных облаков. Развитие радиолокационных методов измерения расстояний между Землёй и планетами, Луной и космическими зондами, а также доплеровских смещений частот дало возможность непосредственно определить значение астрономической единицы в км . В системе астрономических постоянных, принятой в 1964, астрономическая единица равна 149,6 млн. км . Таким образом, в этой системе П. С. является производной астрономической постоянной и составляет 8,794". При этом световая астрономическая единица (время прохождения светом расстояния, равного 1 астрономической единице) принята равной t_а = 499,012 сек , а экваториальный радиус земного сфероида — равным 6378,160 км .

  Лит.: Блажко С. Н., Курс сферической астрономии, 2 изд., М.— Л., 1954; Идельсон Н. И., Фундаментальные постоянные астрономии и геодезии, в кн.: Астрономический ежегодник СССР на 1942 год, М.— Л., 1941, с. 431-34; Куликов К. А., Фундаментальные постоянные астрономии, М., 1956; Фундаментальные постоянные астрономии [Материалы 21 Симпозиума Международного астрономического союза. 21 августа 1961], М., 1967; Lilley Е., Brouwer D., The solar parallax and the hydrogen line, «The Astronomical Journal», 1959, v. 64, №8.

  В. К. Абалакин.

Параллактическая монтировка

Параллакти'ческая монтиро'вка, экваториальная монтировка, монтировка телескопа , имеющая две оси вращения; одна из них направлена на полюс мира, составляя с плоскостью горизонта угол, равный географической широте места установки телескопа. Вторая ось ей перпендикулярна и лежит в плоскости небесного экватора. Оси позволяют поворачивать телескоп и направлять его в нужную точку неба с заданными координатами (часовой угол и склонение). Для слежения за суточным движением звёзд телескоп поворачивается часовым механизмом вокруг полярной оси со скоростью 1 оборот за звёздные сутки.

Параллактическая полигонометрия

Параллакти'ческая полигономе'трия, см. Полигонометрия .

Параллактические движения звёзд

Параллакти'ческие движе'ния звёзд, кажущиеся перемещения звёзд на небесной сфере, обусловленные движением Солнечной системы относительно этих звёзд; являются частью собственных движений звёзд . П. д. з. направлены к точке, называемой антиапексом, которая противоположна на небесной сфере апексу движения Солнца.

Параллактический треугольник

Параллакти'ческий треугольник в астрономии, сферический треугольник на небесной сфере с вершинами в полюсе мира Р , зените Z места наблюдения и данной точке s небесной сферы, в большинстве случаев — центре какого-либо светила (рис. ). В П. т. стороны равны: z , 90°—d и 90°—j (z и d — соответственно зенитное расстояние и склонение точки s, j — широта места наблюдения). Два угла равны t и 360° — А (t и А — соответственно часовой угол и отсчитываемый от севера азимут точки s); третий угол называется параллактическим углом и обозначают q. Применение формул сферической тригонометрии к П. т. позволяет по известным горизонтальным координатам А и z точки s найти её экваториальные координаты t и d, и наоборот:

  cos z = sin j sin d+cos j cos d cos t ;

  sin z cos A = — cos j sin d+sin j cos d cos t ;

  sin z sin A = cos d sin t .

П. т. применяется также для определения моментов и азимутов восхода и захода небесных светил (в этом случае z = 90°), вычисления моментов наступления сумерек и многого другого.

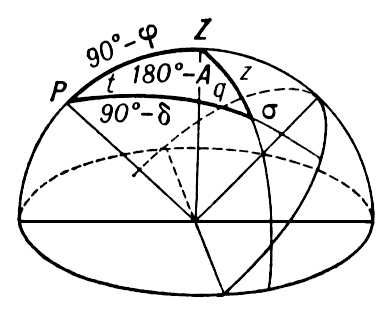
Рис. к ст. Параллактический треугольник.

Параллактический угол

Параллакти'ческий у'гол в астрономии, угол при небесном светиле в параллактическом треугольнике . Отсчитывается против часовой стрелки (для наблюдателя, находящегося внутри сферы) от направления светило — полюс мира.

Параллактический штатив

Параллакти'ческий штати'в, упрощённая параллактическая монтировка телескопа, обычно без отсчётных кругов и часового механизма, но с микрометренными винтами для плавного вращения; используется в небольших (любительских, школьных) телескопах.

Параллелепипед

Параллелепи'пед (греч. parallelepipedon, от parallelos — параллельный и epipedon — плоскость), шестигранник, противоположные грани которого попарно параллельны. П. имеет 8 вершин, 12 рёбер; его грани представляют собой попарно равные параллелограммы. П. называется прямым, если его боковые ребра перпендикулярны к плоскости основания (в этом случае 4 боковые грани— прямоугольники); прямоугольным, если этот П. прямой и основанием служит прямоугольник (следовательно, 6 граней — прямоугольники); П., все грани которого квадраты, называется кубом. Объём П. равен произведению площади его основания на высоту.

Рис. к ст. Параллелепипед.