Лит.: Горелик Г. С., Колебания и волны, 2 изд., М., 1959, гл. Ill, §9; Мандельштам Л. И., Полн. собр. трудов, т. 4, М., 1955 (Лекции по колебаниям, ч. 1, лекции 18—19).

  С. М. Хайкин.

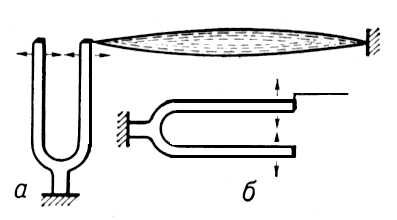
Рис. 1. а — параметрическое возбуждение колебаний струны; б — вынужденное колебание струны.

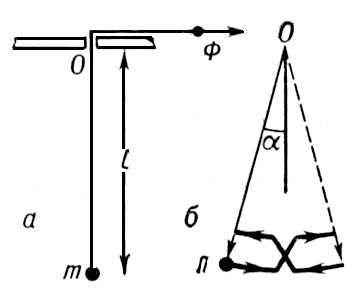
Рис. 2. а — устройство маятника с переменной длиной подвеса; б — схема движения тела маятника за один период.

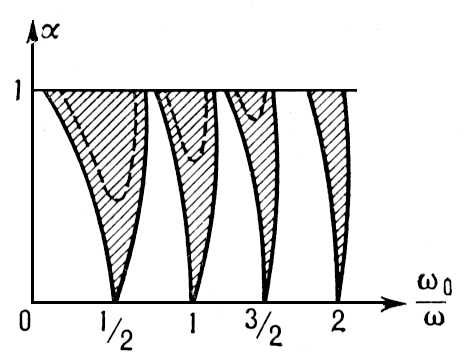
Рис. 3. Области, в которых возможно параметрическое возбуждение колебаний.

Параметрическое представление

Параметри'ческое представле'ние функции, выражение функциональной зависимости между несколькими переменными посредством вспомогательных переменных параметров . В случае двух переменных х и у зависимость между ними F (х , у ) = 0 может быть геометрически истолкована как уравнение некоторой плоской кривой. Любую величину t , определяющую положение точки (х , у ) на этой кривой (например, длину дуги, отсчитываемой со знаком + или — от некоторой точки кривой, принятой за начало отсчёта, или момент времени в некотором заданном движении точки, описывающей кривую), можно принять за параметр, в функции которого выразятся х и у :

  x = j(t ), у = y(t ). (*)

  Последние функции и дадут П. п. функциональной зависимости между х и у , уравнения (*) называют параметрическими уравнениями соответствующей кривой. Так, для случая зависимости x ² + y ² = 1 имеем П. п. х= cos t , у = sin t (0 ? t < 2p) (параметрические уравнения окружности); для случая зависимости х ² —у ² = 1 имеем П. п.

;  (t ¹ 0) или также х = cosec t , y=ctg t (— p< t < p, t ¹ 0) (параметрические уравнения гиперболы). Если параметр t можно выбрать так, что функции (*) рациональны, то кривую называют уникурсальной (см. Уникурсальная кривая ); такой является, например, гипербола. Особенно важно П. п. пространственных кривых, т. е. задание их уравнениями вида: х = j(t ), у = y (t ), z = c (t ). Так, прямая в пространстве допускает П. п. х = а + mt ; у = b + nt ; z = с + pt , винтовая линия — П. п. х = a cos t ; у = a sin t ; z = ct .

  Для случая трёх переменных х , у и z , связанных зависимостью F (x , y , z ) = 0 (одну из них, например z, можно рассматривать как неявную функцию двух других), геометрическим образом служит поверхность. Чтобы определить положение точки на ней, нужны два параметра u и u (например, широта и долгота на поверхности шара), так что П. п. имеет вид: х = j(u, u), у = y (u, u); z = c (u , u). Например, для зависимости x ² + y ² = (z ² +1 )² имеем П. п. х = (u ² —1 ) cos u; у = (u ² + 1) sinu; z = u . Важнейшими преимуществами П. п. являются: 1) то, что они дают возможность изучать неявные функции и в тех случаях, когда переход к их явному заданию без посредства параметров затруднителен; 2) то, что здесь удаётся выражать многозначные функции посредством однозначных. Вопросы П. п. изучены особенно хорошо для аналитических функций. П. п. аналитических функций посредством однозначных аналитических функций составляет предмет теории униформизации .

Параметрон

Параметро'н, элемент автоматики и вычислительной техники, принцип действия которого основан на особенностях параметрического возбуждения и усиления электрических колебаний . Простейший П. представляет собой колебательный контур, настроенный на частоту f . При периодическом изменении под воздействием сигнала накачки с частотой f_н , равной примерно 2f , одного из энергоёмких параметров контура в нём возникает колебание с частотой

, когерентное по отношению к возбуждающему колебанию. При этом фаза возбуждённых в П. колебаний может принимать одно из двух отличающихся на 180° значений, условно обозначаемых (0, p), и сколь угодно долго находиться в этом состоянии. Эта способность П. выбирать одну из двух стабильных фаз называется свойством квантования фазы. П. как логический элемент или ячейка запоминающего устройства был запатентован в 1954 Э. Гото (Япония). На основе П. созданы счётчики, регистры, сумматоры, запоминающие устройства и системы управления ЭВМ.

  По типу нелинейного элемента различают индуктивные П. (с ферритовыми сердечниками, магнитной плёнкой), ёмкостные П. (на параметрических полупроводниковых диодах, сегнетоэлектрических конденсаторах) и резистивные П. (на туннельных и др. полупроводниковых диодах с вольтамперной характеристикой, имеющей падающий участок). Скорость (тактовая частота f _т ) переключения П. пропорциональна частоте накачки и меньше её примерно в 20—50 раз. Наиболее надёжными и дешёвыми являются одноконтурные индуктивные (на ферритовых сердечниках) П. с потребляемой мощностью 15—50 мвт , f _т ? 100 кгц ; более экономичные (3— 6 мвт ) ёмкостные П. на конденсаторах имеют более высокое быстродействие (f _т » 5 Мгц ); ещё больше быстродействие резистивных П., т.к. продолжительность процесса установления колебаний в них соизмерима с периодом собственных колебаний контура. В индуктивных П. на тонких магнитных плёнках или в ёмкостных П. на полупроводниковых диодах тактовая частота достигает 150 Мгц . В связи с разработкой параметрических усилителей и генераторов света появляется принципиальная возможность перехода к частотам оптического диапазона, что должно привести к существенному повышению быстродействия П.

  Лит.: Параметроны. [Сб. ст.], пер. с япон., кн. 1—2, М., 1961—62; Параметроны в цифровых устройствах, М., 1968; Вишневецкий А. И., Немецкий Г. М., Параметроны и их применение в устройствах связи, М., 1968.

  В. И. Медведев.