С. О. Хан-Магомедов (введение, архитектура),
В. И. Ракитин (художественное конструирование, графика, театрально-декорационное искусство),
А. А. Морозов (литература).

А. М. Родченко. Оформление и мебель рабочего клуба, экспонировавшиеся на Международной выставке декоративного искусства в Париже. 1925.

В. Ф. Степанова. Проекты спортивной одежды. Гуашь. 1920-е гг. Собственность В. А. Родченко. Москва.

М. О. Барщ, М. Я. Гинзбург, М. А. Охитович и др. Проект жилого здания («товарищеская коммуна»). 1929.

Н. Д. Колли. Проект трансформаторной станции. 1-я пол. 1920-х гг.

И. И. Леонидов. Проект «Института Ленина» (Института библиотековедения им. В. И. Ленина). 1927. Фрагмент.

М. Я. Гинзбург. Проект дома акционерного общества «Оргметалл» в Москве. 1926—27.

А. А., В. А. и Л. А. Веснины. Проект Дворца Труда в Москве. 1922—23.

А. М. Ган. Киоск Всероссийского комитета помощи инвалидам войны… (слева — в подготовленном для работы виде; справа — в сложенном виде). 1-я пол. 1920-х гг.

Эскизы рисунков для тканей: 1 — В. Ф. Степановой (гуашь, 1924, собрание В. А. Родченко, Москва); 2 — Л. С. Поповой (гуашь, 1924, собрание Д. В. Сарабьянова и Е. Б. Муриной, Москва).
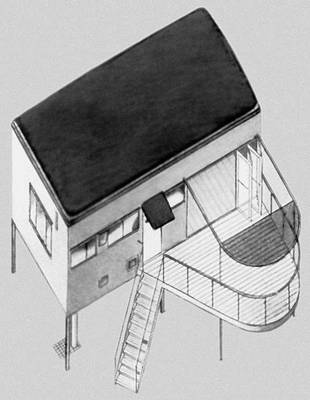
М. О. Барщ, М. Я. Гинзбург, М. А. Охитович и др. Проект однокомнатной ячейки для «семейного коллектива». 1929.

В. А. и Г. А. Стенберги. Экспериментальная конструкция. Металл, стекло. 1919.

И. А. Глосов. Проект клуба им. Зуева в Москве. 1927.

Л. М. Лисицкий. «Ленинская трибуна». Проект. Цветная тушь. 1920—24. Научно-исследовательский музей архитектуры им. А. В. Щусева. Москва.

А. К. Буров. Проект центрального вокзала в Москве. 1925.

Г. Г. Клуцис. «Спорт». Фотомонтаж. 1923.

Л. С. Попова. Макет установки для трагического фарса Кроммелинка «Великодушный рогоносец» в Театре им. В. Э. Мейерхольда в Москве. 1922. Центральный театральный музей им. А. А. Бахрушина. Москва.
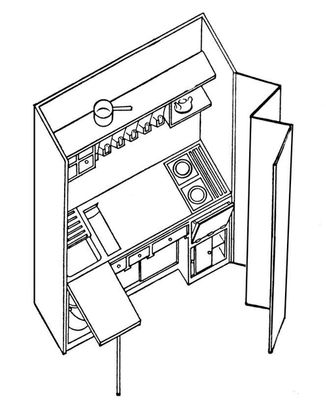
М. О. Барщ, В. Н. Владимиров, М. Я. Гинзбург, А. Л. Пастернак, Г. А. Сум-Шик. Типовой проект шкафа-кухни. 1928—29.
Конструктивная логика
Конструкти'вная ло'гика, логика, развиваемая в соответствии с принципами т. н. конструктивного направления , отличающимися требованием конструктивности (возможности эффективного построения) объектов, существование которых утверждается в высказываниях (предложениях). См. Конструктивные объекты .
Лит. см. при ст. Логика .
Конструктивная математика
Конструкти'вная матема'тика, абстрактная наука о конструктивных процессах, человеческой способности осуществлять их и о их результатах — конструктивных объектах. Абстрактность К. м. проявляется прежде всего в том, что в ней систематически применяются две абстракции: абстракция потенциальной осуществимости и абстракция отождествления. Абстракцию потенциальной осуществимости используют, когда отвлекаются от практических ограничений конструктивных возможностей в пространстве, времени и материале. Абстракцию отождествления используют, когда говорят о двух в том или ином смысле одинаковых объектах как об одном и том же объекте. В К. м. не применяется характерная для теоретико-множественной математики абстракция актуальной бесконечности, связанная с рассмотрением никогда не завершаемых процессов как бесконечно продолженных и тем самым как бы завершенных.
Конструктивный процесс, результатом которого является объект, одинаковый с А, называется построением объекта А . Высказывания, связанные с человеческой способностью осуществлять конструктивные процессы, часто формулируются в К. м. в виде теорем существования, утверждающих, что существует объект, удовлетворяющий каким-то требованиям. Под этим подразумевают, что построение такого объекта потенциально осуществимо, т. е. что владеют способом его построения. Это понимание теорем существования отличается от их понимания в теоретико-множественной математике, что вынуждает строить для К. м. свою логику, отличную от обслуживающей теоретико-множественную математику классической математической логики, — конструктивную математическую логику.
Понятия конструктивного процесса и конструктивного объекта не определяются в К. м. В таких общих определениях и нет надобности, поскольку в К. м. обычно имеют дело не с конструктивными процессами и конструктивными объектами вообще, а с определёнными видами тех и других.
Простейшим видом конструктивных объектов являются слова в фиксированном алфавите, т. е. ряды букв этого алфавита (слово «буква» понимается здесь как «элементарный знак», т. е. как «знак, частями которого мы не интересуемся»; алфавит — это набор букв). Конструктивный процесс, результатом которого является слово, состоит в данном случае в выписывании этого слова буква за буквой. Частным случаем слов являются натуральные числа, которые мы рассматриваем как слова в алфавите 01, начинающиеся с нуля и, кроме того, нуля не содержащие, т. е. как слова 0, 01, 011, 0111,... Добавляя к этому алфавиту знак минус «—» и знак дроби «/», получают возможность строить рациональные числа как некоторые слова в алфавите 01 — /. Т. о., рациональные числа оказываются конструктивными объектами.
Естественно, возник вопрос о построении действительных чисел в рамках К. м. и, далее, вопрос о включении математического анализа в эти рамки. Эти цели достигнуты на основе уточнённого понятия алгоритма . Каким из известных уточнений этого понятия (Тьюринга машина , рекурсивные функции, нормальные алгорифмы) здесь пользоваться, при этом несущественно. В дальнейшем под «алгорифмом» будет пониматься нормальный алгорифм .
Конструктивной последовательностью рациональных (натуральных) чисел будет называться алгорифм, перерабатывающий всякое натуральное число в рациональное (натуральное) число. Без существенного ограничения общности можно считать конструктивную последовательность рациональных чисел алгорифмом в алфавите 01 — /ab. Запись такого алгорифма будет осуществляться как слово в алфавите 01. О конструктивной последовательности рациональных чисел