Криволинейные координаты на поверхности. Изложенная идея применима без всяких изменений и к введению криволинейных К. на произвольной поверхности. Например, для случая долготы j и широты q на сфере линиями j = const являются меридианы, а линиями q = const — широтные круги, расположение которых всем хорошо известно из элементов географии. Криволинейные, или, как их иначе называют, гауссовы, К. на произвольной поверхности являются основным аппаратом дифференциальной геометрии поверхностей.

  Однородные координаты на плоскости. Евклидова плоскость, дополненная бесконечно удалёнными элементами, может рассматриваться с проективной точки зрения как замкнутая поверхность (см. Проективная плоскость ), на которой бесконечно удалённые точки не играют какой-либо особой роли. На всей проективной плоскости введение К., характеризующих положение точки парой чисел (u, u) с сохранением взаимной однозначности и непрерывности соответствия, невозможно. Вместо этого пользуются однородными К. При этом каждой точке ставятся в соответствие не пары, а тройки чисел (x₁ , x₂ , x₃ ), причём двум тройкам (x₁ , x₂ , x₃ ) и (x₁ ^’ , x₂ ^’ , x₃ ^’ ) соответствует одна и та же точка только тогда, когда входящие в них числа пропорциональны, т. е. существует такой множитель l, что

x₁ ^’ = lx₁ , x₂ ^’ = lx₂ , x₃ ^’ = lx₃ .

Такие системы координат играют большую роль в геометрии.

  Координаты точки в пространстве. Аффинные, или общие декартовы, К. в трёхмерном пространстве вводятся заданием точки О и трёх векторов

, , , не лежащих в одной плоскости. Для получения К. х, у, z точки Р вектор

  представляют в виде

= xex+ уе_у +ze_z .

В простейшем случае прямоугольных К. векторы e_x , е_у , e_z попарно перпендикулярны и имеют единичную длину. В пространстве возможны два существенно различных типа систем прямоугольных К.: правая система (где е_у и e_z лежат в плоскости чертежа, а e_x направлен вперёд, к читателю) и левая система (где e_x и e_z лежат в плоскости чертежа, а е_у направлен к читателю).

  В пространстве пользуются также системами криволинейных К., общая схема которых такова: в какой-либо области G пространства рассматриваются три функции точки u (P), u(P), w(P), подчинённые условию, чтобы через каждую точку Р области G проходила одна поверхность семейства u = const , одна поверхность семейства u = const и одна поверхность семейства w = const . Тем самым каждой точке ставятся в соответствие три числа (u, u, w) — её К. Поверхности, определяемые уравнениями u = const, или u = const, или w = const , называют координатными.

  В приложениях (к механике, математической физике и пр.) наиболее употребительны некоторые специальные системы криволинейных К., а именно: сферические координаты , цилиндрические координаты .

  Координаты прямой, плоскости и т. п. Принцип двойственности (см. Двойственности принцип ), устанавливающий равноправность точек и прямых в геометрии двух измерений и равноправность точек и плоскостей в геометрии трёх измерений, подсказывает ту мысль, что с помощью особых К. могут быть определены положения прямых и плоскостей. Действительно, если, например, в прямоугольных К. уравнение прямой (не проходящей через начало К.) приведено к виду ux + uy + 1 = 0, то числами u и u (u = -¹ /_a , u = -¹ /_b , где а и b суть «отрезки», отсекаемые прямой на осях) вполне определяется положение прямой; можно принять (u, u ) за К. (так называемые тангенциальные К.) прямой линии. Симметричность уравнения ux + uy + 1 = 0 относительно пар (х, у) и (u, u) является аналитическим выражением принципа двойственности. Вполне аналогично случаям n = 2 (плоскость, поверхность) и n = 3 (трёхмерное пространство) употребление К. в n-мepном пространстве.

  Лит. см. при ст. Аналитическая геометрия .

  А. Н. Колмогоров.

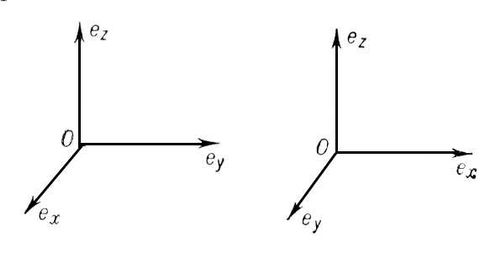
Рис. 3 (слева) и рис. 4 (справа) к ст. Координаты.

Рис. 1 (слева) и рис. 2 (справа) к ст. Координаты.

Координационно-вычислительный центр

Координацио'нно-вычисли'тельный центр, часть командно-измерительного комплекса , предназначенный для проведения расчётов, связанных с полётом космических кораблей (вывод корабля на орбиту, изменение траектории полёта, коррекция орбиты и др.). К.-в. ц. обрабатывает данные, полученные с корабля, и анализирует их. К.-в. ц. оснащен быстродействующими универсальными ЦВМ.

Координационное число

Координацио'нное число' в кристаллографии, число ближайших к данному атому или иону соседних одинаковых атомов или ионов в кристалле. Прямые линии, соединяющие центры ближайших атомов или ионов в кристалле, образуют координационный многогранник, в центре которого находится данный атом. Одному и тому же К. ч. могут соответствовать разные многогранники. В структурах алмаза , кремния , германия , сфалерита К. ч. равно 4, а координационный многогранник — тетраэдр. В структуре NaCI каждый ион Na окружен шестью ионами Cl, а каждый ион Cl — шестью ионами Na, т. е. для обоих типов ионов К. ч. равно 6, многогранник — октаэдр. В структуре флюорита CaF₂ для ионов Са К. ч. равно 8, многогранник — куб; для ионов F К. ч. равно 4, многогранник — тетраэдр. Наивысшее возможное К. ч. равно 12, что характерно для металлов с плотнейшей кубической или гексагональной упаковкой. Для металлов с объёмно-центрированной решёткой К. ч. равно 8. Для полупроводниковых кристаллов, не имеющих плотнейшей упаковки атомов, характерны К. ч., равные 4 или 6.

  В химии К. ч. — число атомов или атомных групп, непосредственно присоединённых к данному атому в комплексных соединениях . Понятие К. ч. применяется также при описании структуры жидкостей и аморфных тел. В этом случае К. ч. — среднее число ближайших соседей атома, оно может быть дробным. К. ч. является мерой ближнего порядка в жидкостях и аморфных телах (см. Жидкость , Аморфное состояние , Дальний порядок и ближний порядок ).

  Лит. см. при ст. Кристаллохимия .

  М. П. Шаскольская.